| MATLAB Function Reference | |
表示
[N,D] = rat(X) [N,D] = rat(X,tol) rat(...) S = rats(X,strlen) S = rats(X)
詳細
すべての浮動小数点数が有理数であっても、それを分母と分子が共に小さな整数である分数を使って単純な有理数に近似したほうが良い場合があります。rat は、これを行う関数です。有理数近似は、連分数展開で作られます。rats は rat をコールし、文字列を出力します。
[N,D] = rat(X)
1.e-6*norm(X(:),1) の範囲で、N./D が、X を近似するような配列 N と D を出力します。
[N,D] = rat(X,tol)
tol の範囲で、N./D が X を近似するような N と D を出力します。
rat(X) は、出力引数がなければ、単純に連分数を表示します。
S = rats(X,strlen)
X の要素の単純な有理数近似を含む文字列を出力します。割り当てられたスペースに出力できず、X の他の要素と比較して無視できない要素には、アスタリスクが使われます。strlenは、rats が出力する文字列の要素の長さです。デフォルトは、strlen = 13 で、78 カラムに、6 要素を表示することができます。
S = rats(X)
format rat で出力する結果と同じ結果を出力します。
例題
s = 1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7
s =
0.7595
format rat
rats(s)
s =
319/420
これは、簡単な有理数です。この分母は 420 で、オリジナルの式の分母の項の最小公倍数になっています。s の値が2進浮動小数点数として内部に保存されても、求めたい有理数の形式に復元できます。
rat(s) を実行します。
1 + 1/(-4 + 1/(-6 + 1/(-3 + 1/(-5))))
[n,d] = rat(s)
n = 319, d = 420
数学での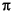 
の値は、明らかに有理数ではありません。しかし、MATLABの 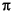を近似した pi の値は有理数です。IEEE 浮動小数点演算では、pi は、つぎのように大きな整数値と 252との比になります。
14148475504056880/4503599627370496
しかし、これは簡単な有理数ではありません。format rat 、または、rats(pi) を使って、pi を出力した値は、つぎのようになります。
355/113
この近似は、Euclid's time として知られているものです。この10進表現は、
3.14159292035398
rat(pi)
3 + 1/(7 + 1/(16))
この結果で、355/113 がどのようにして得られたものかわかります。精度が悪くなりますが、よく知られたπの近似として、22/7 があります。これは、この連分数の最初の2項から得られたものです。
アルゴリズム
rat(X) は、つぎの形式の連分数で、X の各要素を近似します。
d は、繰り返して整数部を取り出して、分数部分の逆数を取ることで求められます。近似の精度は、項数に応じて指数的に良くなり、X = sqrt(2) の場合に最悪になります。 x = sqrt(2) に対する誤差は、項数が k 個で、およそ 2.68*(.173)^k となります。近似の精度は項を 1 つ追加するごとに、10 進数の 1 桁より小さい程度良くなります。浮動小数点数の全精度を得るためには、項数は、21 個必要となります。
参考
| | rank | rbbox | |