MATLAB Function Reference

qr

直交三角分解

表示

[Q,R] = qr(A)
[Q,R,E] = qr(A)
[Q,R] = qr(A,0)
[Q,R,E] = qr(A,0)
R = qr(A)          (sparse matrices)
[C,R] = qr(A,B)    (sparse matrices)
R = qr(A,0)        (sparse matrices)
[C,R] = qr(A,B,0)  (sparse matrices)
X = qr(A)

詳細

関数 qr は、行列の直交三角分解を実行します。この分解は、正方行列でも長方行列でも有効です。これは実数の直交行列または複素ユニタリ行列と、上三角行列との積として行列を表現します。

[Q,R] = qr(A) は、A = Q*R となるような A と同じ次元の上三角行列 R とユニタリ行列 Q を出力します。スパース行列の場合、Q は、ほとんどの要素がゼロになります。

[Q,R,E] = qr(A) は、A*E= Q*R となるような置換行列 E と、対角要素を降順に並べた上三角行列 R と、ユニタリ行列 Q を出力します。abs(diag(R)) が降順になるように置換行列 E の列が選択されます。

[Q,R] = qr(A,0) と [Q,R,E] = qr(A,0) は、メモリを節約した分解を行います。ここで、E は、置換ベクトルで、Q*R = A(:,E) になります。列置換 E は、abs(diag(R)) を小さい順にならべたものです。

R = qr(A) は、スパース行列に対して、上三角行列 R のみを出力します。行列 R は、正規方程式に関連した行列に対して、コレスキ分解を行います。

R'*R = A'*A

は、このアプローチは、A'*A の計算の中で、数値情報の損失を避けます。

[C,R] = qr(A,B) は、スパース行列に対して、直交変換を B に適用し、Q を計算しないで、C = Q'*B を作成します。

R = qr(A,0) と [C,R] = qr(A,B,0) は、スパース行列に対して、メモリの節約になります。

スパース行列に対して、Q-less QR 分解は、スパースな最小二乗問題の解になります。

は、つぎの2つのステップに分けられます。

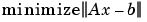
[C,R] = qr(A,b)
x = R\c

A が、スパースで、正方でない場合、MATLAB は、バックスラッシュ演算子を使った線形方程式x = A\bを解く場合、上の2ステップを使います。

X = qr(A) は、LAPACK サブルーチンDGEQRF、または、ZGEQRF のいずれかを使います。triu(qr(A)) は、R になります。

例題

つぎの行列から始めます。

A =
     1     2     3
     4     5     6
     7     8     9
    10    11    12

これは、フルランクの行列ではありません。すなわち、真ん中の列が、両側の列を平均したものです。フルランクでない行列であることは、因子分解でわかります。

[Q,R] = qr(A)

Q =

    -0.0776    -0.8331     0.5444     0.0605
    -0.3105    -0.4512    -0.7709     0.3251
    -0.5433    -0.0694    -0.0913    -0.8317
    -0.7762     0.3124     0.3178     0.4461

R =

    -12.8841    -14.5916    -16.2992
           0     -1.0413     -2.0826
           0           0      0.0000
           0           0           0

R の三角形構造は、対角要素の下はゼロです。すなわち、R(3,3) の中の対角要素上のゼロは、R が、フルランクでない、すなわち、A が、フルランクでないことを示しています。

QR 因子分解は、未知数の数より多い式をもった線形システムを解くために使われます。たとえば、つぎのようにします。

b =

    1
    3
    5
    7

線形システム Ax = b は、3つの未知数に対して、4つの方程式をもっています。最小二乗の意味での最適な解は、次式で計算されます。

x = A\b

結果、つぎの出力を得ます。

Warning: Rank deficient, rank = 2, tol = 1.4594E-014
x =
    0.5000
          0
    0.1667

量 tol は、R の対角要素を無視できるか否かを決定する許容誤差です。[Q,R,E] = qr(A) の場合、

tol = max(size(A))*eps*abs(R(1,1))

となります。解 x は、分解とつぎの 2 ステップ

y = Q'*b;
x = R\y

計算された解は、Ax の型でチェックできます。これは、丸め誤差の範囲内で、b と等しくなります。これは、連立方程式 Ax = b が、過決定やランク落ちの場合でさえ、うまく解けることを示しています。無限数の解ベクトル x が存在します。すなわち、QR 分解は、それらの解の一つを見つけただけです。

アルゴリズム

関数 qr は、QR 分解を計算する LAPACK ルーチンを使っています。

シンタックス	実数	複素数
R = qr(A) R = qr(A,0)	DGEQRF	ZGEQRF
[Q,R] = qr(A) [Q,R] = qr(A,0)	DGEQRF, DORGQR	ZGEQRF, ZUNGQR
[Q,R,e] = qr(A) [Q,R,e] = qr(A,0)	DGEQPF, DORGQR	ZGEQPF, ZUNGQR

参考

lu, null, orth, qrdelete, qrinsert

代数演算子 \ と /

参考文献

Anderson, E., Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen, LAPACK User's Guide, Third Edition, SIAM, Philadelphia, 1999.

qmr

qrdelete