eig (MATLAB Function 参考文献)

固有値と固有ベクトル

表示

d = eig(A)
d = eig(A,B)
[V,D] = eig(A)
[V,D] = eig(A,'nobalance')
[V,D] = eig(A,B)
[V,D] = eig(A,B,flag)

詳細

d = eig(A) は、行列 A の固有値からなるベクトルを出力します。

d = eig(A,B) は、A と Bが、正方行列の場合、一般化した固有値を含むベクトルを計算します。

[V,D] = eig(A) は、A*V = V*Dとなるような、行列 A の固有値からなる行列(D) と固有ベクトルからなる行列(V) を出力します。行列D は、A の正準形で、主対角上にA の固有値をもつ行列です。行列 V は、モーダル行列で、各列がA の固有ベクトルです。

eig(A) に対して、固有ベクトルは、各ノルムが1.0 になるようにスケーリングされます。[W,D] = eig(A.'); W = W.'を使って、 W*A = D*W を満たす左固有ベクトルを計算します。

[V,D] = eig(A,'nobalance') は、バランス化を行わずに、固有値と固有ベクトルを計算します。通常、バランス化は、入力行列の条件数を改良し、より正確な固有ベクトルと固有値の計算を可能にします。しかし、丸め誤差の影響を受けるような小さな値の要素が行列に含まれていると、バランス化によって、オリジナルの行列の他の要素と同じくらい重要となるようにスケーリングされるので、間違った固有ベクトルが出力されることがあります。このような場合は、nobalanceオプションを使ってください。詳細は、関数balance を参照してください。

[V,D] = eig(A,B) は、A*V = B*V*D となるような、一般固有値からなる対角行列D と各列が対応する固有ベクトルからなる行列 Vを出力します。固有ベクトルは、各ノルムが 1.0 とになるようにスケーリングされます。

[V,D] = eig(A,B,flag) は、固有値と固有ベクトルを計算するために使用するアルゴリズムを指定します。flag は、つぎのいずれかを設定することができます。

'chol'
Bのコレスキー分解を使って、A と B の一般化固有値を計算します。この方法は、対称(エルミート)Aと対称(エルミート)正定Bに対するデフォルトの方法です。

'qz'
対称性が無視される場合、可能ならば、非対称(非エルミート)のA と B に対して、QZ アルゴリズムを使います。

`'chol'`	`B`のコレスキー分解を使って、`A` と `B` の一般化固有値を計算します。この方法は、対称(エルミート)`A`と対称(エルミート)正定`B`に対するデフォルトの方法です。
`'qz'`	対称性が無視される場合、可能ならば、非対称(非エルミート)の`A` と `B` に対して、QZ アルゴリズムを使います。

注意

固有値問題は、方程式のnontrivialな解を決定するものです。

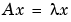
ここで、A は、n 行 n 列の行列で、 x は、長さ n の列ベクトル、は、スカラです。方程式を満足するの n 個の値は固有値で、xの対応する値は、右固有ベクトルです。MATLABの中で、関数eigは、固有値に対して解きます。そして、オプションとして、固有ベクトルxについても解きます。

一般的な 固有値問題は、つぎの方程式のnontrivialな解を決定するものです。

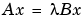
ここで、A と B は、n 行 n 列の行列で、はスカラです。方程式を満足するの値は、一般化固有値であり、x の対応する値は、一般化右固有ベクトルになります。

B が正則の場合、問題は、標準の固有値問題

に直して、解くことができます。

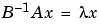
B は、特異になる可能性があるので、別のアルゴリズム、QZ法が、必要になります。

行列に重根の固有値がなり場合、固有ベクトルは、必ず独立で、固有ベクトル行列V は、相似変換を適用された場合、オリジナル行列 A を対角化したものになります。しかし、行列に重根の固有値が存在する場合、固有ベクトルのフル(独立な)集合をもたない限り、対角行列とはなりません。固有ベクトルが独立でない場合、オリジナル行列は、欠落(defective)と言います。行列が、defectiveな場合、eig からの解は、A*X = X*Dを満足します。

例題

行列

B = [3 -2 -.9 2*eps;-2 4 -1 -eps;-eps/4 eps/2 -1 0;-.5 -.5 .1 1];

は、丸め誤差の範囲の要素をもっています。正しい固有値を計算するためには、nobalanceオプションが必要であることを示す例題です。つぎのステートメントを試してください。

[VB,DB] = eig(B)
B*VB - VB*DB
[VN,DN] = eig(B,'nobalance')
B*VN - VN*DN

アルゴリズム

MATLAB は、LAPACK のルーチンを使って、固有値と固有ベクトルを計算します。

ケース
ルーチン

1
Aが実数の対称行列
DSYEV

2
Aが実数の非対称行列

予備的な平衡化ステップ
DGEEV

d = eig(A,'nobalance')
DGEHRD, DHSEQR

[V,D] = eig(A,'nobalance')
DGEHRD, DORGHR, DHSEQR, DTREVC

3
エルミート A 行列
ZHEEV

4
非エルミート A 行列

予備的な平衡化ステップ
ZGEEV

d = eig(A,'nobalance')
ZGEHRD, ZHSEQR

[V,D] = eig(A,'nobalance')
ZGEHRD, ZUNGHR, ZHSEQR, ZTREVC

5
A は、実数対称、
Bは、対称正定行列。特殊ケース：
DSYGV

実数行列 A、B に対して eig(A,B,'qz')
DGGEV (case 6)

6
Aは実数の非対称、
Bは、実数一般行列
DGGEV

7
A は、複素数エルミート行列、B は、エルミート正定行列。
特殊ケース：
ZHEGV

A、または、Bが複素数の場合、eig(A,B,'qz')
ZGGEV (case 8)

8
A は、複素非エルミート行列、Bは、複素行列
ZGGEV

ケース	ルーチン
1	`A`が実数の対称行列	`DSYEV`
2	`A`が実数の非対称行列
		予備的な平衡化ステップ	`DGEEV`
		`d = eig(A,'nobalance')`	`DGEHRD`, `DHSEQR`
		`[V,D] = eig(A,'nobalance')`	`DGEHRD`, `DORGHR`, `DHSEQR`, `DTREVC`
3	エルミート `A` 行列	`ZHEEV`
4	非エルミート `A` 行列
		予備的な平衡化ステップ	`ZGEEV`
		`d = eig(A,'nobalance')`	`ZGEHRD`, `ZHSEQR`
		`[V,D] = eig(A,'nobalance')`	`ZGEHRD`, `ZUNGHR`, `ZHSEQR`, `ZTREVC`
5	`A` は、実数対称、 `B`は、対称正定行列。特殊ケース：	`DSYGV`
		実数行列 `A`、`B` に対して `eig(A,B,'qz')`	`DGGEV` (case 6)
6	`A`は実数の非対称、 `B`は、実数一般行列	`DGGEV`
7	`A` は、複素数エルミート行列、`B` は、エルミート正定行列。特殊ケース：	`ZHEGV`
		`A`、または、`B`が複素数の場合、`eig(A,B,'qz')`	`ZGGEV` (case 8)
8	`A` は、複素非エルミート行列、`B`は、複素行列	`ZGGEV`

参考

balance, condeig, hess, qz, schur

参考文献

Anderson, E., Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen, LAPACK User's Guide, Third Edition, SIAM, Philadelphia, 1999.

edit eigs