MATLAB Function Reference

del2

離散ラプラシアン

表示

L = del2(U)
L = del2(U,h)
L = del2(U,hx,hy)
L = del2(U,hx,hy,hz,...)

定義

行列Uが、正方格子上の点で評価される関数u(x,y)とみなせる場合、4*del2(U)は、ラプラス微分演算子をuに用いたときの有限差分近似になります。

ここで、

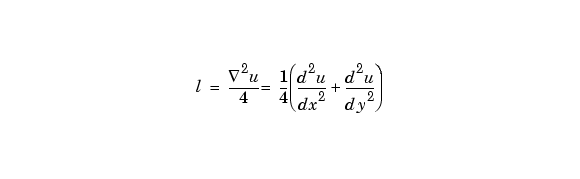
で、内部にあります。エッジでは、同じ式がキュービック補間に適用されます。

より多くの変数をもつ関数 u(x,y,z,...) に対しては、del2(U)は近似になります。

ここで、Nはuの変数の数です。

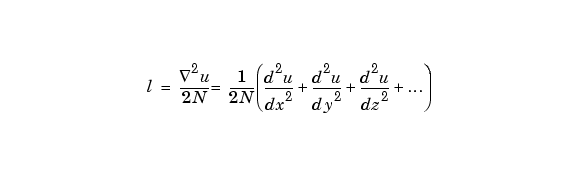
詳細

L = del2(U) は、Uが長方形配列のとき、

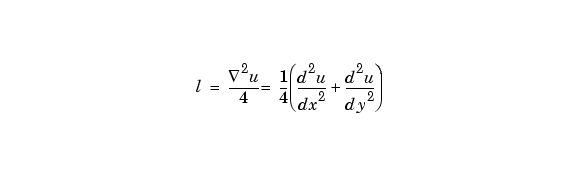
の離散近似になります。行列Lは、各要素がUの要素と、隣接する4つの要素の平均との差に等しく、Uと同じサイズです。

L = del2(U) は、Uが多次元配列のとき、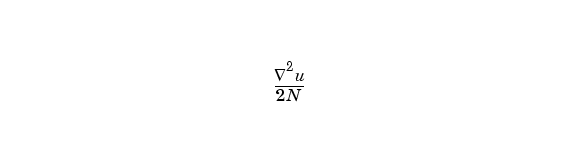

の近似を出力します。

ここで、Nは、ndims(u)です。

L = del2(U,h) は、Hがスカラのとき、各方向(デフォルトでは、H = 1)での点の間隔として、Hを使用します。

L = del2(U,hx,hy) は、Uが長方形配列のとき、hxとhyで指定した間隔を使用します。hxがスカラの場合、x方向の点の間の間隔になります。hxがベクトルの場合、長さはsize(u,2)で、点数で、x座標を指定しなければなりません。同様に、hyがスカラの場合、y方向の点の間の間隔を与えます。hyがベクトルの場合、長さはsize(u,1)で、点数で、y座標を指定しなければなりません。

L = del2(U,hx,hy,hz,...) は、Uが多次元のとき、hx, hy, hz, ...で与えられた間隔を使用します。

例題

関数

は、

この関数に対して、4*del2(U)は、4です。

[x,y] = meshgrid(-4:4,-3:3);
U = x.*x+y.*y  
U =
    25     18     13     10      9     10     13     18     25
    20     13      8      5      4      5      8     13     20
    17     10      5      2      1      2      5     10     17
    16      9      4      1      0      1      4      9     16
    17     10      5      2      1      2      5     10     17
    20     13      8      5      4      5      8     13     20
    25     18     13     10      9     10     13     18     25

V = 4*del2(U)
V =
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4
     4      4      4      4      4      4      4      4      4

参考

diff, gradient

default4

delaunay