MATLAB Function Reference

beta, betainc, betaln

Beta 関数

表示

B = beta(Z,W)
I = betainc(X,Z,W)
L = betaln(Z,W)

定義

Beta 関数は、つぎの式で表わされます。

ここで、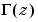は、Gamma 関数です。不完全 Beta 関数は、つぎの式で表わされます。

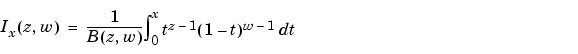
詳細

B = beta(Z,W) は、複素数配列 Zと W の対応する要素に対して、Beta 関数を計算します。配列は同じサイズでなければなりません（または、一方はスカラでも構いません）。

I = betainc(X,Z,W) は、不完全Beta 関数を計算します。 X の要素は閉区間 [0,1] 内でなければなりません。

L = betaln(Z,W) は、beta(Z,W)を計算せずに、Beta 関数の自然対数 log(beta(Z,W))を計算します。Beta 関数は非常に大きな値から非常に小さな値までを変動できるので、関数の対数は非常に有効となることがあります。

例題

format rat 
beta((0:10)',3)

ans =

     1/0 
     1/3 
     1/12 
     1/30 
     1/60 
     1/105 
     1/168 
     1/252 
     1/360 
     1/495 
     1/660 

この場合、整数引数を用いているので

beta(n,3)
= (n-1)!*2!/(n+2)!
= 2/(n*(n+1)*(n+2))

は、完全な最小整数の比になり、有理数書式は正確な結果を得ることができます。

IEEE演算のコンピュータでは、x = 510に対して betaln(x,x) = -708.8616 となり、log(realmin)よりわずかに小さくなります。従って、beta(x,x) は、アンダーフロー（または異常値）となります。

アルゴリズム

beta(z,w) = exp(gammaln(z)+gammaln(w)-gammaln(z+w))
betaln(z,w) = gammaln(z)+gammaln(w)-gammaln(z+w)

besselj, bessely

bicg