

| MATLAB Function Reference |   |
表示
J = besselj(nu,Z) 1種の Bessel 関数
Y = bessely(nu,Z) 2種の Bessel 関数
J = besselj(nu,Z,1)
Y = bessely(nu,Z,1)
[J,ierr] = besselj(nu,Z)
[Y,ierr] = bessely(nu,Z)
定義
微分方程式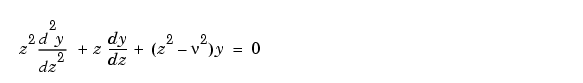
は、Bessel方程式と言われ、この解がBessel関数として知られています。ここで、 は、非負の定数です。
は、非負の定数です。
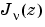 と
と 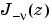 は、
は、 の整数でないものに対するBessel方程式の基本解を形作ります。
の整数でないものに対するBessel方程式の基本解を形作ります。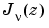 は、
は、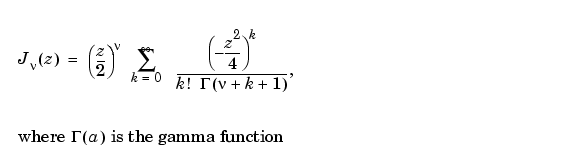
により定義されます。
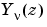 は、
は、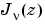 に線形独立で、つぎのように定義されるBessel方程式の2番目の解です。
に線形独立で、つぎのように定義されるBessel方程式の2番目の解です。

詳細
J = besselj(nu,Z)
は、複素数配列Zの各々の要素に対して、第一種のBessel関数 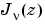 を計算します。次数
を計算します。次数nu は、整数である必要はありませんが、実数でなければなりません。引数Zは、複素数でも構いません。求まる結果は、Zが、正のところで実数になります。
nu と Z が、同じ大きさの配列の場合、結果も同じ大きさになります。入力のどちらかがスカラの場合、要素がすべてその値を示し、大きさが他の引数と同じ大きさの配列として取り扱います。一つの入力が行ベクトルで、他の引数が列ベクトルの場合、結果は2次元の関数値テーブルになります。
Y = bessely(nu,Z)
は、実数で、非負の次数nuと引数Zをもつ第二種Bessel関数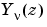 を計算します。
を計算します。
J = besselj(nu,Z,1)
besselj(nu,Z).*exp(-imag(Z))を計算します。
Y = bessely(nu,Z,1)
は、bessely(nu,Z).*exp(-imag(Z))を計算します。
[J,ierr] = besselj(nu,Z) と [Y,ierr] = bessely(nu,Z)
は、エラーフラグの配列も出力します。
ierr = 1 |
|
ierr = 2 |
|
ierr = 3 |
|
ierr = 4 |
|
ierr = 5 |
注意
Bessel関数は、第三種Bessel関数であるHankel関数と密接な関係があります。

ここで、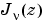 は、
は、besseljで、 は、
は、besselyです。Hankel関数もBessel方程式の基本解を形作ります(besselhを参照)。
例題
format long
z = (0:0.2:1)';
besselj(1,z)
ans =
0
0.09950083263924
0.19602657795532
0.28670098806392
0.36884204609417
0.44005058574493
bessely(1,z)
ans =
-Inf
-3.32382498811185
-1.78087204427005
-1.26039134717739
-0.97814417668336
-0.78121282130029
besselj(3:9,(0:.2,10)') は、Abramowitz and Stegun著のHandbook of Mathematical Functionsの398ページに記載されいる表を作成します。
bessely(3:9,(0:.2,10)') は、Abramowitz and Stegun著の Handbook of Mathematical Functionsの399ページに記載されている表を作成します。
アルゴリズム
関数besselj と besselyは、D. E. Amos [3] [4]により作成されたライブラリを使うFortran MEX-ファイルを使います。
参考
参考文献
[1] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, National Bureau of Standards, Applied Math. Series #55, Dover Publications, 1965, sections 9.1.1, 9.1.89 and 9.12, formulas 9.1.10 and 9.2.5.
[2] Carrier, Krook, and Pearson, Functions of a Complex Variable: Theory and Technique, Hod Books, 1983, section 5.5.
[3] Amos, D. E., "A Subroutine Package for Bessel Functions of a Complex Argument and Nonnegative Order," Sandia National Laboratory Report, SAND85-1018, May, 1985.
[4] Amos, D. E., "A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order," Trans. Math. Software, 1986.
 | besseli, besselk | beta, betainc, betaln |  |