Mathematics

差分方程式とフィルタリング

MATLABは、差分方程式とフィルタ操作に対応する関数を用意しています。これらの関数は、基本的には、ベクトルに作用します。

ベクトルは、信号処理やデータ解析に対して、サンプルホールド信号または連続信号を扱うのに使います。多入力システムに対して、行列の行は、行列の列として表現される入力をもつサンプル点に対応します。

関数   

y = filter(b, a, x)

は、ベクトルaとbにより記述されたフィルタでベクトルxのデータを処理し、フィルタ出力yを作成します。

filterコマンドは、差分方程式を効果的に実行したものと考えることができます。フィルタの構造は、つぎのような差分方程式で記述される一般的に有限の遅れをもつものとして表現されます。ここで、nは、カレントサンプルのインデックスで、naはベクトルaにより記述される多項式の次数で、nbはベクトルbにより記述される多項式の次数です。出力y(n)は、カレントとその前の入力x(n) x(n-1) ...と前の出力y(n-1) y(n-2) ....の線形結合です。

.

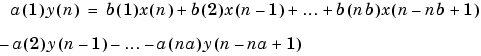例えば、4時間の窓を考えて、平均的な交通量を見るために移動平均フィルタを交通量データcountに適用してスムージングします。このプロセスは、つぎの差分方程式で表されます。

対応するベクトルは、つぎのようになります。

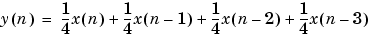
a = 1;
b = [1/4 1/4 1/4 1/4];

つぎのコマンドを実行して、ワークスペースに行列countを作成します。

load count.dat

この例題では、交通量の最初の列を取り出して、ベクトルxとします。

x = count(:,1);

データの4時間の移動平均を

y = filter(b,a,x);

で効率良く計算します。オリジナルデータとスムージングしたデータとを重ね書きして比べます。

t = 1:length(x);
plot(t,x,'-.',t,y,'-'), grid on
legend('Original Data','Smoothed Data',2)

実線で表示されるフィルタリングされたデータは、点線で表される観測された交通量の4時間移動平均です。

実際的なフィルタリングの適用に対して、Signal Processing Toolboxは、フィルタを設計したり、解析したりする多くの関数を用意しています。

Basic Fitting インタフェース

フーリエ解析と高速フーリエ変換 (FFT)