Mathematics

行列のベキと指数

この節は、つぎの行列のベキと指数をMATLABの中で計算する方法を説明します。

• 正の整数
• 逆数と分数
• 要素単位
• 指数

正の整数のベキ

Aが正方行列で、pが正の整数ならば、A^pは、A自身をp回乗算します。

X = A^2

X =
     3     6    10
     6    14    25
    10    25    46

逆数と分数のベキ乗

Aが正方行列で、非正則ならば、A^(-p)は、inv(A)をp回乗算します。

Y = B^(-3)

Y =
    0.0053   -0.0068    0.0018
   -0.0034    0.0001    0.0036
   -0.0016    0.0070   -0.0051

A^(2/3)のような分数のべき乗もまた可能です。結果は、行列の固有値の分布に依存します。

要素単位のベキ乗

要素単位のべき乗は、.^で実行されます。例えば、

X = A.^2

A =
     1     1     1
     1     4     9
     1     9    36    

指数

関数

sqrtm(A)

は、より正確なアルゴリズムを使って、A^(1/2)を計算します。sqrtmの　mは、要素単位に機能するA.^(1/2)のようなsqrt(A)と区別する関数です。

線形、定数係数、常微分方程式システムは、つぎにように表現されます。

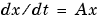
ここで、x = x(t)はtの関数ベクトルで、Aはtに独立な行列です。解は、行列指数として表現されます。

関数

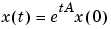
expm(A)

は、行列指数を計算します。つぎの3行3列の係数行列を考えます。

A =
     0    -6    -1
     6     2   -16
    -5    20   -10

そして、初期条件x(0)をつぎのように考えます。

x0 =
     1
     1
     1

行列指数は、0 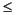t 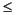1 の範囲で、101点で微分方程式の解x(t)を計算するために使います。

X = [];
for t = 0:.01:1
   X = [X expm(t*A)*x0]; 
end

3次元位相空間プロットが得られます。

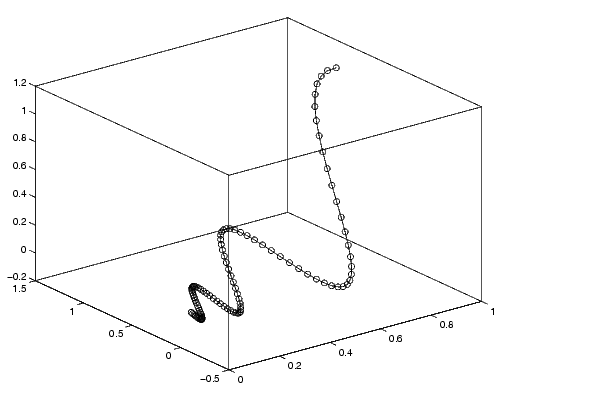
plot3(X(1,:),X(2,:),X(3,:),'-o')

これは、解が原点に向かって螺旋状になることを示しています。この挙動は、つぎの節で述べる係数行列の固有値に関連しています。

QR 因子分解

固有値