

| Mathematics |   |
QR 因子分解
直交行列、または、直交性の列をもつ行列は、各列が単位長さをもち、お互いが直交関係になる実数行列に分解されます。Qが直交であれば、
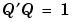
になります。最も簡単な直交行列は、2次元の座標回転変換に使うものです。
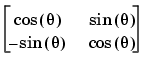
複素数行列に対して、対応する項はユニタリです。直交ユニタリ行列は、長さと角度が保存され、そのため誤差が大きくならないので、数値計算に対して望ましいものです。
直交またはQR因子分解は、任意の直交行列を一つの直交行列またはユニタリ行列と一つの上三角行列の積で表現します。列の並べ替えも含まれています。
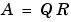
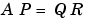
で、ここで、Qは直交またはユニタリ行列で、Rは上三角行列で、Pは並べ替え行列です。
QR因子分解には、フルサイズ、エコノミサイズ、列置換をもつもの、もたないものと、4つの種類があります。
過多線形システムは、列よりも多くの行をもつ長方形行列を含んでいます。すなわち、m行n列で、m > nです。フルサイズQR因子分解は、m行m列の正方直交行列Qとm行n列上三角行列Rの積になります。
[Q,R] = qr(C)
Q =
-0.8182 0.3999 -0.4131
-0.1818 -0.8616 -0.4739
-0.5455 -0.3126 0.7777
R =
-11.0000 -8.5455
0 -7.4817
0 0
多くの場合、Qの最後のm - n列は、Rの下部にゼロを乗算することになるので、必要ありません。エコノミサイズのQR因子分解は、直交要素をもつm行n列の長方形行列Qと正方n行n列の上三角行列Rの積で表されます。ここでの3行2列の例題では、あまり大きな影響はありません。しかし、非常に大きい長方形行列ならば、時間とメモリの節約になり、このことが最も重要なことになります。
[Q,R] = qr(C,0)
Q =
-0.8182 0.3999
-0.1818 -0.8616
-0.5455 -0.3126
R =
-11.0000 -8.5455
0 -7.4817
LU因子分解と比べ、QR因子分解は、ピポッドや並べ替えを必要としません。しかし、オプションの列の並び替えは、設定した三番目の引数に出力され、非正則を見つけたり、ランク落ちを調べるのに有効です。因子分解の各々のステップで、大きなノルムをもつ残りの分解されていない行列の列が、そのステップでの基底として使われます。これは、Rの対角要素が減少する順番になり、列の間である線形依存性がこれらの要素を調べることにより、表現されます。ここで使っている小さな行列の例題に対して、Cの2番目の列は1番目の列のノルムよりも大きいノルムをもちます。それで、二つの列を交換します。
[Q,R,P] = qr(C)
Q =
-0.3522 0.8398 -0.4131
-0.7044 -0.5285 -0.4739
-0.6163 0.1241 0.7777
R =
-11.3578 -8.2762
0 7.2460
0 0
P =
0 1
1 0
エコノミサイズと列の並び替えを組み合わせたとき、3番目の引数は、並べ替え行列でなく、並べ替えベクトルになります。
[Q,R,p] = qr(C,0)
Q =
-0.3522 0.8398
-0.7044 -0.5285
-0.6163 0.1241
R =
-11.3578 -8.2762
0 7.2460
p =
2 1
QR因子分解は、過多線形システムを等価な三角システムに変換します。表現
norm(A*x - b)
norm(Q*R*x - b)
直交行列の乗算は、ユークリッドノルムを保存するので、この表現は、つぎのものとも等価です。
norm(R*x - y)
ここで、y = Q'*bです。Rの最後のm-n行はゼロなので、この表現は、2つの部分に分けられます。
norm(R(1:n,1:n)*x - y(1:n))
norm(y(n+1:m))
Aがフルランクのとき、xに対して解くことができ、最初のものはゼロです。それで、2番目のものは残差のノルムを与えます。Aがフルランクでないとき、Rの三角構造は、最小二乗問題に対する基本解を探します。
 | LU 因子分解 | 行列のベキと指数 |  |