Mathematics

コレスキ因子分解

コレスキ因子分解は、対称行列を三角行列とその転置行列との積として表現します。

ここで、Rは、上三角行列です。

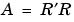
対称行列すべてが、この方法で分解できることはありません。すなわち、因子分解による行列は正定行列です。これは、Aの対角要素は正で、非対角要素は"あまり大きくない"ものです。Pascal行列は、興味のある例題です。この章を通して、例題の行列Aは、3行3列のPascal行列です。ちょっと、一時的ですが、6行6列の行列を考えましょう。

A = pascal(6)

A =
       1     1     1     1     1     1
       1     2     3     4     5     6
       1     3     6    10    15    21
       1     4    10    20    35    56
       1     5    15    35    70   126
       1     6    21    56   126   252

Aの要素は、二項係数になります。各々の要素は、その上と左の要素の和になります。コレスキ因子分解は、つぎのようになります。

R = chol(A)

R =
     1     1     1     1     1     1
     0     1     2     3     4     5
     0     0     1     3     6    10
     0     0     0     1     4    10
     0     0     0     0     1     5
     0     0     0     0     0     1

要素は、再び、二項係数になっています。R'*RがAに等しいことは、二項係数の積の和を含んでいることを示すものです。

コレスキ因子分解は、複素数行列にも適用できます。コレスキ因子分解を行なった複素数行列はA' = Aを満足し、Hermitian positive definiteと言われます。

線形システム

A*x = b

は、

R'*R*x = b

で置き換えることで、コレスキ因子分解を行なうことができます。バックスラッシュ演算子は、三角システムで使えるので、つぎのようにして簡単に解くことができます。

x = R\(R'\b)

Aが、n行n列の行列の場合、chol(A)の計算の誤差はO(n³)になりますが、連続バックスラッシュによる解の誤差は、たったO(n²)です。

LU, QR, コレスキ因子分解

LU 因子分解