Graphics

3次元ステムプロット

stem3は、xy平面から伸びる3次元ステムプロットを表示します。MATLABは1つのベクトル引数を使って、引数が列ベクトルか行ベクトルかに応じて、x = 1かまたはy = 1で1行のステムをプロットします。stem3は、2次元表示では、視覚化できないデータを表示する目的をもっています。

例題 - FFT の 3-次元ステムプロット

たとえば、高速フーリエ変換は複素平面上の単位円周上の点で計算されます。したがって、単位円周上でプロットを視覚化することは有意義です。単位円

th = (0:127)/128*2*pi;
x = cos(th);
y = sin(th);

とステップ関数の周波数応答を計算し、

f = abs(fft(ones(10,1),128));

終端に塗りつぶしたダイアモンド形のマーカ記号をもつ3次元ステムプロットを使って、データを表示します。

stem3(x,y,f','d','fill')
view([-65 30])

 

グラフへのラベル付け

つぎのステートメントでグラフにラベルを付けます。

xlabel('Real')
ylabel('Imaginary')
zlabel('Amplitude')
title('Magnitude Frequency Response')

表示方向を変更するには、マウスベースの3次元回転モードをonに設定します。

rotate3d on

例題 - ステムプロットとラインプロットの組み合わせ

3次元ステムプロットは、多数のデータ点を出力しないで、離散関数を視覚化する場合に有効です。たとえば、stem3を使って、特定の定数sに対するLaplace変換基本関数3次元ステムプロットは、多数のデータ点を出力しないで、離散関数を視覚化する場合に有効です。たとえば、stem3を使って、特定の定数sに対するLaplace変換基本関数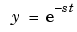を視覚化することができます。を視覚化することができます。

t = 0:.1:10;% 時間範囲
s = 0.1+i;% ラセン率
y = exp(-s*t);% 指数的な減衰を計算

ステムの機能を少し改良したものを示します。tを時間と共に大きさが増大する高さをもつラセンを作成し、ステムプロットをします。そして、ステムの各シンボルを繋ぐ曲線を描きます。

stem3(real(y),imag(y),t)
hold on
plot3(real(y),imag(y),t,'r')
hold off
view(-39.5,62)

 

グラフのラベル

つぎのステートメントで軸ラベルを付加します。

xlabel('Real')
ylabel('Imaginary')
zlabel('Magnitude')

ラインプロットとステムプロットとの組み合わせ

階段状プロット