

| Embedded Target for Texas Instruments C6000 DSPs |   |
Filter a scalar input using least-mean-square adaptive filtering
Library
Description
The LMS Adaptive FIR block performs least-mean-square (LMS) adaptive filtering. This filter is implemented using a direct form structure.
The following constraints apply to the inputs and outputs of this block:
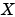 must be a Q.15 data type.
must be a Q.15 data type.
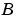 must be a Q.15 data type.
must be a Q.15 data type.
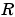 is a Q1.30 data type.
is a Q1.30 data type.
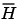 has length equal to the number of filter taps and is a Q.15 data type. The number of filter taps must be a positive, even integer.
has length equal to the number of filter taps and is a Q.15 data type. The number of filter taps must be a positive, even integer.
This block performs LMS adaptive filtering according to the equations
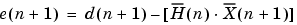
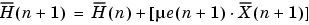
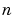 designates the time step.
designates the time step.
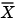 is a vector composed of the current and last
is a vector composed of the current and last 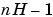 scalar inputs.
scalar inputs.
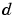 is the desired signal. The output
is the desired signal. The output 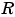 converges to
converges to 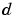 as the filter converges.
as the filter converges.
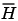 is a vector composed of the current set of filter taps.
is a vector composed of the current set of filter taps.
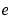 is the error, or
is the error, or 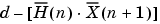 .
.
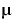 is the step size.
is the step size.
For this block, the input 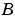 and the output
and the output 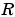 are defined by
are defined by
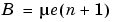
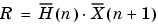
which combined with the first two equations, result in the following equations that this block follows:
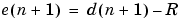
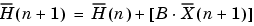
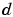 and
and 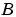 must be produced externally to the LMS Adaptive FIR block. See Examples below for a sample model where this is done.
must be produced externally to the LMS Adaptive FIR block. See Examples below for a sample model where this is done.
The LMS Adaptive FIR block supports discrete sample times and both little-endian and big-endian code generation.
Dialog Box
Algorithm
In simulation, the LMS Adaptive FIR block is equivalent to the TMS320C62x DSP Library assembly code function DSP_firlms2. During code generation, this block calls the DSP_firlms2 routine to produce optimized code.
Examples
The following model uses the LMS Adaptive FIR block.
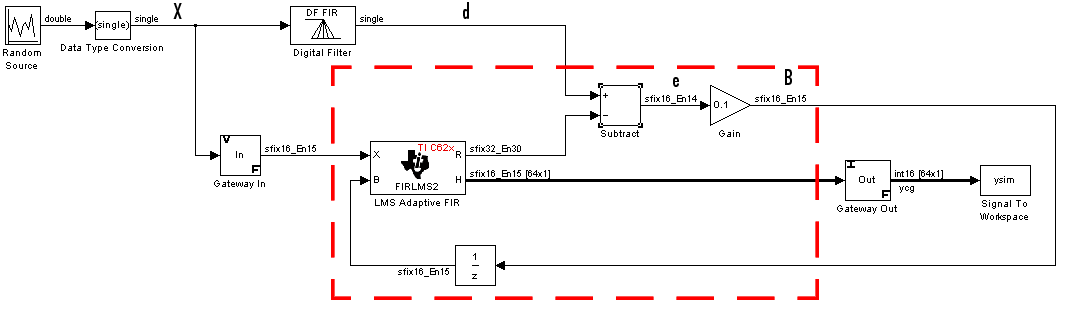
The portion of the model enclosed by the dashed line produces the signal 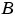 and feeds it back into the LMS Adaptive FIR block. The inputs to this region are
and feeds it back into the LMS Adaptive FIR block. The inputs to this region are 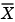 and the desired signal
and the desired signal 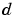 , and the output of this region is the vector of filter taps
, and the output of this region is the vector of filter taps 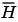 . Thus this region of the model acts as a canonical LMS adaptive filter. For example, compare this region to the
. Thus this region of the model acts as a canonical LMS adaptive filter. For example, compare this region to the adaptlms function in the Filter Design Toolbox. adaptlms performs canonical LMS adaptive filtering and has the same inputs and output as the outlined section of this model.
To use the LMS Adaptive FIR block you must create the input 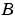 in some way similar to the one shown here. You must also provide the signals
in some way similar to the one shown here. You must also provide the signals 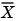 and
and 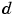 . This model simulates the desired signal
. This model simulates the desired signal 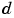 by feeding
by feeding 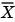 into a digital filter block. You can simulate your desired signal in a similar way, or you may bring
into a digital filter block. You can simulate your desired signal in a similar way, or you may bring 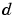 in from the workspace with a From Workspace or codec block.
in from the workspace with a From Workspace or codec block.
 | General Real FIR | Matrix Multiply |  |