Symbolic Math Toolbox

Limits

The fundamental idea in calculus is to make calculations on functions as a variable "gets close to" or approaches a certain value. Recall that the definition of the derivative is given by a limit

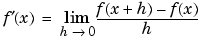
provided this limit exists. The Symbolic Math Toolbox allows you to compute the limits of functions in a direct manner. The commands

• syms h n x
  limit( (cos(x+h) - cos(x))/h,h,0 )
  

which return

• ans =
  -sin(x)
  

and

• limit( (1 + x/n)^n,n,inf )
  

which returns

• ans =
  exp(x)
  

illustrate two of the most important limits in mathematics: the derivative (in this case of cos x) and the exponential function. While many limits

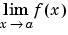
are "two sided" (that is, the result is the same whether the approach is from the right or left of a), limits at the singularities of 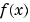are not. Hence, the three limits

yield the three distinct results: undefined, , and 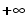, respectively.

In the case of undefined limits, the Symbolic Math Toolbox returns NaN (not a number). The command

• limit(1/x,x,0)
  

or

• limit(1/x)
  

returns

• ans =
  NaN
  

The command

• limit(1/x,x,0,'left')
  

returns

• ans =
  -inf
  

while the command

• limit(1/x,x,0,'right')
  

returns

• ans =
  inf
  

Observe that the default case, limit(f) is the same as limit(f,x,0). Explore the options for the limit command in this table. Here, we assume that f is a function of the symbolic object x.

Mathematical Operation	MATLAB Command
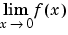	limit(f)
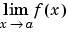	limit(f,x,a) or limit(f,a)
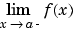	limit(f,x,a,'left')
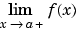	limit(f,x,a,'right')

Calculus

Integration