Symbolic Math Toolbox

Calculus

The Symbolic Math Toolboxes provide functions to do the basic operations of calculus; differentiation, limits, integration, summation, and Taylor series expansion. The following sections outline these functions.

Differentiation

Let's create a symbolic expression:

• syms a x     
  f = sin(a*x)
  

Then

• diff(f)
  

differentiates f with respect to its symbolic variable (in this case x), as determined by findsym:

• ans =
  cos(a*x)*a
  

To differentiate with respect to the variable a, type

• diff(f,a)
  

which returns :

• ans =
  cos(a*x)*x
  

To calculate the second derivatives with respect to x and a, respectively, type

• diff(f,2)
  

or

• diff(f,x,2)
  

which returns

• ans =
  -sin(a*x)*a^2
  

and

• diff(f,a,2)
  

which returns

• ans =
  -sin(a*x)*x^2
  

Define a, b, x, n, t, and theta in the MATLAB workspace, using the sym command. The table below illustrates the diff command.

f	diff(f)
x^n	x^n*n/x
sin(a*t+b)	cos(a*t+b)*a
exp(i*theta)	i*exp(i*theta)

To differentiate the Bessel function of the first kind, besselj(nu,z), with respect to z, type

• syms nu z
  b = besselj(nu,z);
  db = diff(b)
  

which returns

• db =
  -besselj(nu+1,z)+nu/z*besselj(nu,z)
  

The diff function can also take a symbolic matrix as its input. In this case, the differentiation is done element-by-element. Consider the example

• syms a x
  A = [cos(a*x),sin(a*x);-sin(a*x),cos(a*x)]
  

which returns

• A =
  [  cos(a*x),  sin(a*x)]
  [ -sin(a*x),  cos(a*x)]
  

The command

• diff(A)
  

returns

• ans =
  [ -sin(a*x)*a,  cos(a*x)*a]
  [ -cos(a*x)*a, -sin(a*x)*a]
  

You can also perform differentiation of a column vector with respect to a row vector. Consider the transformation from Euclidean (x, y, z) to spherical 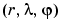coordinates as given by 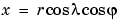, , 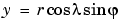and 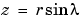. Note that 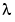corresponds to elevation or latitude while 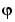denotes azimuth or longitude.

To calculate the Jacobian matrix, J, of this transformation, use the jacobian function. The mathematical notation for J is

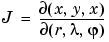
For the purposes of toolbox syntax, we use l for 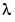and f for 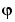. The commands

• syms r l f
  x = r*cos(l)*cos(f); y = r*cos(l)*sin(f); z = r*sin(l);
  J = jacobian([x; y; z], [r l f])
  

return the Jacobian

• J =
  [    cos(l)*cos(f), -r*sin(l)*cos(f), -r*cos(l)*sin(f)]
  [    cos(l)*sin(f), -r*sin(l)*sin(f),  r*cos(l)*cos(f)]
  [           sin(l),         r*cos(l),                0]
  

and the command

• detJ = simple(det(J))
  

returns

• detJ = 
  -cos(l)*r^2
  

Notice that the first argument of the jacobian function must be a column vector and the second argument a row vector. Moreover, since the determinant of the Jacobian is a rather complicated trigonometric expression, we used the simple command to make trigonometric substitutions and reductions (simplifications). The section Simplifications and Substitutions discusses simplification in more detail.

A table summarizing diff and jacobian follows.

Mathematical Operator	MATLAB Command
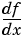	diff(f) or diff(f,x)
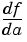	diff(f,a)
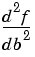	diff(f,b,2)
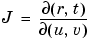	J = jacobian([r:t],[u,v])

Using the Symbolic Math Toolbox

Limits