Symbolic Math Toolbox

Symbolic and Numeric Conversions

Consider the ordinary MATLAB quantity

• t = 0.1
  

The sym function has four options for returning a symbolic representation of the numeric value stored in t. The 'f' option

• sym(t,'f')
  

returns a symbolic floating-point representation

• '1.999999999999a'*2^(-4)
  

The 'r' option

• sym(t,'r')
  

returns the rational form

• 1/10
  

This is the default setting for sym. That is, calling sym without a second argument is the same as using sym with the 'r' option:

• sym(t)
   
  ans =
  1/10
  

The third option 'e' returns the rational form of t plus the difference between the theoretical rational expression for t and its actual (machine) floating-point value in terms of eps (the floating-point relative accuracy):

• sym(t,'e')
   
  ans =
  1/10+eps/40
  

The fourth option 'd' returns the decimal expansion of t up to the number of significant digits specified by digits:

• sym(t,'d')
   
  ans =
  .10000000000000000555111512312578
  

The default value of digits is 32 (hence, sym(t,'d') returns a number with 32 significant digits), but if you prefer a shorter representation, use the digits command as follows:

• digits(7)
  sym(t,'d')
   
  ans =
  .1000000
  

A particularly effective use of sym is to convert a matrix from numeric to symbolic form. The command

• A = hilb(3)
  

generates the 3-by-3 Hilbert matrix:

• A =
   
      1.0000    0.5000    0.3333
      0.5000    0.3333    0.2500
      0.3333    0.2500    0.2000
  

By applying sym to A

• A = sym(A)
  

you can obtain the (infinitely precise) symbolic form of the 3-by-3 Hilbert matrix:

• A =
   
  [   1, 1/2, 1/3]
  [ 1/2, 1/3, 1/4]
  [ 1/3, 1/4, 1/5]
  

Constructing Real and Complex Variables

The sym command allows you to specify the mathematical properties of symbolic variables by using the 'real' option. That is, the statements

• x = sym('x','real'); y = sym('y','real');
  

or more efficiently

• syms x y real
  z = x + i*y
  

create symbolic variables x and y that have the added mathematical property of being real variables. Specifically this means that the expression

• f = x^2 + y^2
  

is strictly nonnegative. Hence, z is a (formal) complex variable and can be manipulated as such. Thus, the commands

• conj(x), conj(z), expand(z*conj(z))
  

return the complex conjugates of the variables

• x, x-i*y, x^2+y^2
  

The conj command is the complex conjugate operator for the toolbox. If conj(x) == x returns 1, then x is a real variable.

To clear x of its "real" property, you must type

• syms x unreal
  

or

• x = sym('x','unreal')
  

The command

• clear x
  

does not make x a nonreal variable.

Creating Abstract Functions

If you want to create an abstract (i.e., indeterminant) function 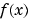, type

• f = sym('f(x)')
  

Then f acts like 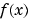and can be manipulated by the toolbox commands. To construct the first difference ratio, for example, type

• df = (subs(f,'x','x+h') - f)/'h'
  

or

• syms x h
  df = (subs(f,x,x+h)-f)/h
  

which returns

• df =
  (f(x+h)-f(x))/h
  

This application of sym is useful when computing Fourier, Laplace, and z-transforms.

Using sym to Access Maple Functions

Similarly, you can access Maple's factorial function k!, using sym:

• kfac = sym('k!')
  

To compute 6! or n!, type

• syms k n
  subs(kfac,k,6), subs(kfac,k,n)
   
  ans =
  720
  
  ans =
  n!
  

Or, if you want to compute, for example, 12!, simply use the prod function

• prod(1:12)
  

Example: Creating a Symbolic Matrix

A circulant matrix has the property that each row is obtained from the previous one by cyclically permuting the entries one step forward. We create the circulant matrix A whose elements are a, b, and c, using the commands

• syms a b c
  A = [a b c; b c a; c a b]
  

which return

• A = 
  [ a, b, c ]
  [ b, c, a ]
  [ c, a, b ]
  

Since A is circulant, the sum over each row and column is the same. Let's check this for the first row and second column. The command

• sum(A(1,:))
  

returns

• ans =
  a+b+c
  

The command

• sum(A(1,:)) == sum(A(:,2)) % This is a logical test.
  

returns

• ans =
       1
  

Now replace the (2,3) entry of A with beta and the variable b with alpha. The commands

• syms alpha beta;
  A(2,3) = beta;
  A = subs(A,b,alpha)
  

return

• A = 
  [     a, alpha,     c]
  [ alpha,     c,  beta]
  [     c,     a, alpha]
  

From this example, you can see that using symbolic objects is very similar to using regular MATLAB numeric objects.

The Default Symbolic Variable

When manipulating mathematical functions, the choice of the independent variable is often clear from context. For example, consider the expressions in the table below.

Mathematical Function	MATLAB Command
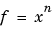	f = x^n
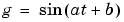	g = sin(a*t + b)
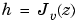	h = besselj(nu,z)

If we ask for the derivatives of these expressions, without specifying the independent variable, then by mathematical convention we obtain 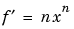, , 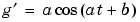and

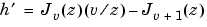. Let's assume that the independent variables in these three expressions are 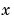, , 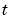and 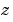, respectively. The other symbols, 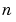, , 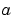, 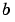and 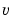, are usually regarded as "constants" or "parameters." If, however, we wanted to differentiate the first expression with respect to 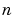, for example, we could write

to get .

By mathematical convention, independent variables are often lower-case letters found near the end of the Latin alphabet (e.g., x, y, or z). This is the idea behind findsym, a utility function in the toolbox used to determine default symbolic variables. Default symbolic variables are utilized by the calculus, simplification, equation-solving, and transform functions. To apply this utility to the example discussed above, type

• syms a b n nu t x z
  f = x^n; g = sin(a*t + b); h = besselj(nu,z);
  

This creates the symbolic expressions f, g, and h to match the example. To differentiate these expressions, we use diff.

• diff(f)
  

returns

• ans =
  x^n*n/x
  

See the section Differentiation for a more detailed discussion of differentiation and the diff command.

Here, as above, we did not specify the variable with respect to differentiation. How did the toolbox determine that we wanted to differentiate with respect to x? The answer is the findsym command

• findsym(f,1)
  

which returns

• ans =
  x
  

Similarly, findsym(g,1) and findsym(h,1) return t and z, respectively. Here the second argument of findsym denotes the number of symbolic variables we want to find in the symbolic object f, using the findsym rule (see below). The absence of a second argument in findsym results in a list of all symbolic variables in a given symbolic expression. We see this demonstrated below. The command

• findsym(g)
  

returns the result

• ans =
  a, b, t
  

Note    The default symbolic variable in a symbolic expression is the letter that is closest to 'x' alphabetically. If there are two equally close, the letter later in the alphabet is chosen.

Here are some examples.

Expression	Variable Returned by findsym
x^n	x
sin(a*t+b)	t
besselj(nu,z)	z
w*y + v*z	y
exp(i*theta)	theta
log(alpha*x1)	x1
y*(4+3*i) + 6*j	y
sqrt(pi*alpha)	alpha

Creating Symbolic Variables and Expressions

Creating Symbolic Math Functions