Spline Toolbox

Approximation to Coefficients as Functions of x

To get an actual surface, we now have to go a step further. Look at the coefficients coefsy of the spline in sp:

• coefsy = fnbrk(sp,'c');
  

Abstractly, you can think of the spline in sp as the function

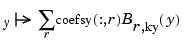
with the 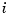th entry 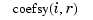of the vector coefficient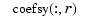 corresponding to 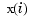, all 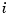. This suggests approximating each coefficient vector 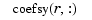by a spline of the same order kx and with the same appropriate knot sequence knotsx. Again for no particular reason, we choose this time to use cubic splines with four uniformly spaced interior knots:

• kx = 4; knotsx = augknt([0:.2:1],kx); 
  sp2 = spap2(knotsx,kx,x,coefsy.');
  

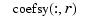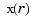Note that spap2(knots,k,x,fx) expects fx(:,j) to be the datum at x(j), i.e., expects each column of fx to be a function value. Since we wanted to fit the datum at , all 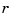, we had to present spap2 with the transpose of coefsy.

The Bivariate Approximation

Now consider the transpose of the coefficients cxy of the resulting spline curve:

• coefs = fnbrk(sp2,'c').';
  

It provides the bivariate spline approximation

to the original data

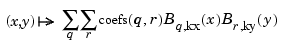
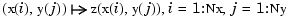
To plot this spline surface over a grid, e.g., the grid

• xv = 0:.025:1; yv = 0:.025:1;
  

you can do the following:

• values = spcol(knotsx,kx,xv)*coefs*spcol(knotsy,ky,yv).'; 
  mesh(xv,yv,values.'), view(150,50);
  

This results in the following figure.

Figure 2-20: Spline Approximation to Franke's Function

This makes good sense since spcol(knotsx,kx,xv) is the matrix whose 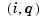th entry equals the value 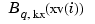at 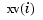of the 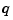th B-spline of order kx for the knot sequence knotsx.

Since the matrices spcol(knotsx,kx,xv) and spcol(knotsy,ky,yv) are banded, it may be more efficient, though perhaps more memory-consuming, for large xv and yv to make use of fnval, as follows:

• value2 = ... 
    fnval(spmak(knotsx,fnval(spmak(knotsy,coefs),yv).'),xv).';
  

This is, in fact, what happens internally when fnval is called directly with a tensor product spline, as in

• value2 = fnval(spmak({knotsx,knotsy},coefs),{xv,yv});
  

Here is the calculation of the relative error, i.e., the difference between the given data and the value of the approximation at those data sites as compared with the magnitude of the given data:

• errors = z - spcol(knotsx,kx,x)*coefs*spcol(knotsy,ky,y).'; 
  disp( max(max(abs(errors)))/max(max(abs(z))) ) 
  0.0539
  

This is perhaps not too impressive. On the other hand, we used only a coefficient array of size

• disp(size(coefs)) 
  8 6
  

to fit a data array of size

• disp(size(z)) 
  15 11
  

Least Squares Approximation as Function of y

Switch in Order