Spline Toolbox

Least Squares Approximation as Function of y

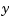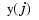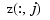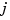We treat these data as coming from a vector-valued function, namely, the function of whose value at is the vector , all . For no particular reason, we choose to approximate this function by a vector-valued parabolic spline, with three uniformly spaced interior knots. This means that we choose the spline order and the knot sequence for this vector-valued spline as

• ky = 3; knotsy = augknt([0,.25,.5,.75,1],ky);
  

and then use spap2 to provide us with the least squares approximant to the data:

• sp = spap2(knotsy,ky,y,z);
  

In effect, we are finding simultaneously the discrete least squares approximation from to each of the Nx data sets

In particular, the statements

• yy = [-.1:.05:1.1]; vals = fnval(sp,yy);
  

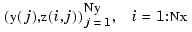
provide the array vals, whose entry 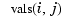can be taken as an approximation to the value 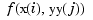of the underlying function 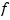at the mesh-point 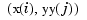since 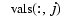is the value at 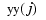of the approximating spline curve in sp.

This is evident in the following figure, obtained by the command:

• mesh(x,yy,vals.'), view(150,50)
  

Note the use of vals.', in the mesh command, needed because of the MATLAB matrix-oriented view when plotting an array. This can be a serious problem in bivariate approximation since there it is customary to think of 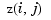as the function value at the point 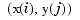, while MATLAB thinks of 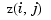as the function value at the point .

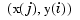Figure 2-19: A Family of Smooth Curves Pretending to Be a Surface

Note that both the first two and the last two values on each smooth curve are actually zero since both the first two and the last two sites in yy are outside the basic interval for the spline in sp.

Note also the ridges. They confirm that we are plotting smooth curves in one direction only.

Choice of Sites and Knots

Approximation to Coefficients as Functions of x