Spline Toolbox

Switch in Order

The approach followed here seems biased, in the following way. We first think of the given data z as describing a vector-valued function of 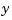, and then we treat the matrix formed by the vector coefficients of the approximating curve as describing a vector-valued function of .

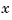What happens when we take things in the opposite order, i.e., think of z as describing a vector-valued function of 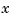, and then treat the matrix made up from the vector coefficients of the approximating curve as describing a vector-valued function of ?

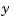Perhaps surprisingly, the final approximation is the same, up to roundoff. Here is the numerical experiment.

Least Squares Approximation as Function of x

First, we fit a spline curve to the data, but this time with 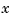as the independent variable, hence it is the rows of z that now become the data values. Correspondingly, we must supply z.', rather than z, to spap2,

• spb = spap2(knotsx,kx,x,z.');
  

thus obtaining a spline approximation to all the curves 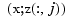. In particular, the statement

• valsb = fnval(spb,xv).';
  

provides the matrix valsb, whose entry 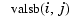can be taken as an approximation to the value 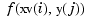of the underlying function 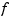at the mesh-point 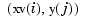. This is evident when we plot valsb using mesh:

• mesh(xv,y,valsb.'), view(150,50)
  
  
  

Figure 2-21: Another Family of Smooth Curves Pretending to Be a Surface

Note the ridges. They confirm that we are, once again, plotting smooth curves in one direction only. But this time the curves run in the other direction.

Approximation to Coefficients as Functions of x

Approximation to Coefficients as Functions of y