Spline Toolbox

stform

A function in stform can be put together from its center sequence centers and its coefficient sequence coefs by the command

• f = stmak(centers, coefs, type);
  

with the string type one of 'tp00', 'tp10', 'tp01', to indicate, respectively, a thin-plate spline, a first partial of a thin-plate spline with respect to the first argument, and a first partial of a thin-plate spline with respect to the second argument. There is one other choice, 'tp'; it denotes a thin-plate spline without any polynomial part and is likely to be used only during the construction of a thin-plate spline, as in tpaps.

A function 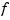in stform depends linearly on its coefficients, meaning that

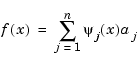
with 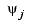either a translate of the basis function 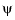or else some polynomial. Suppose you wanted to determine these coefficients 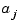so that the function 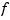matches prescribed values at prescribed sites 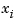. Then you would need the collocation matrix 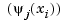. You can obtain this matrix by the command stcol(centers,x,type). In fact, since the stform has 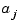as the 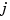th column, coefs(:,j), of its coefficient array, it is worth noting that stcol can also supply the transpose of the collocation matrix. Thus, the command

• values = coefs*stcol(centers,x,type,'tr');
  

would provide the values at the entries of x of the st function specified by centers and type.

The stform is attractive since, in contrast to piecewise polynomial forms, its complexity is the same in any number of variables. It is quite simple, yet, because of the complete freedom in the choice of centers, very flexible and adaptable.

On the negative side, the most attractive choices for a radial basis function share with the thin-plate spline that the evaluation at any site involves all coefficients. For example, plotting a scalar-valued thin-plate spline via fnplt involves evaluation at a 51-by-51 grid of sites, a nontrivial task when there are 1000 coefficients or more. The situation is worse when we want to determine these 1000 coefficients so as to obtain the stform of a function that matches function values at 1000 data sites, as this calls for solving a full linear system of order 1000, a task requiring O(10^9) flops if done by a direct method. Just the construction of the collocation matrix for this linear system (by stcol) takes O(10^6) flops.

The command tpaps, which constructs thin-plate spline interpolants and approximants, uses iterative methods when there are more than 728 data points, but convergence of such iteration may be slow.

The stform

Use