Spline Toolbox

fnbrk

Name and part(s) of a form

Syntax

• out = fnbrk(f,part)
  g = fnbrk(f,[a b])
  pp = fnbrk(pp,j)
  fnbrk(f)
  

Description

out = fnbrk(f,part) returns the part of the form in f specified by part. These are the parts used when the form was put together, in spmak or ppmak or rsmak or stmak, but also other parts derived from these. In particular, out = fnbrk(f,'form') returns a string indicating the form contained in f.

You only need to specify the beginning character(s) of the revelant string.

Regardless of what particular form f is in, part can be one of the following.

'dim'	The dimension of the function's target
'var'	The dimension of the function's domain
'coefs'	The coefficients in that particular form
'interval'	The basic interval of that form

Depending on the form in f, additional parts may be asked for.

If f is in B-form (or BBform or rBform), then additional choices for part are

'knots'	The knot sequence
'coefs'	The B-spline coefficients
'number'	The number of coefficients
'order'	The polynomial order of the spline

.

If f is in ppform (or rpform), then additional choices for part are

'breaks'	The break sequence
'coefs'	The local polynomial coefficients
'pieces'	The number of polynomial pieces
'order'	The polynomial order of the spline
'guide'	The local polynomial coefficients, but in the form needed for PPVALU in PGS

.

If the function in f is multivariate, then the corresponding multivariate parts are returned. This means, e.g., that knots, breaks, and the basic interval, are cell arrays, the coefficient array is, in general, higher than two-dimensional, and order, number and pieces are vectors.

If f is in stform, then additional choices for part are.

'centers'	The centers
'coefs'	The coefficients
'number'	Number of coefficients or terms
'type'	The particular type

g = fnbrk(f,[a b]) does not return a particular part. Rather, it returns a description of the univariate function described by f and in the same form but with the basic interval changed, to the interval given. If the function in f is 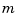-variate, then the desired basic interval must be given by a cell array with 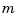entries, with the 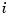th entry specifying the desired interval in the 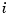th dimension.

pp = fnbrk(pp,j) , with pp the ppform of a univariate function and j a positive integer, does not return a particular part, but returns the ppform of the jth polynomial piece of the function in pp. If pp is the ppform of an 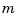-variate function, then j must be a cell array of length 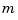. In that case, each entry of j must be a positive integer or else an interval, to single out a particular polynomial piece or else to specify the basic interval in that dimension.

fnbrk(f) returns nothing, but a description of the various parts of the form is printed at the command line instead.

Examples

If p1 and p2 contain the B-form of two splines of the same order, with the same knot sequence, and the same target dimension, then

• p1plusp2 = spmak(fnbrk(p1,'k'),fnbrk(p1,'c')+fnbrk(p2,'c'));
  

provides the (pointwise) sum of those two functions.

If pp contains the ppform of a bivariate spline with at least four polynomial pieces in the first variable, then ppp=fnbrk(pp,{4,[-1 1]}) gives the spline that agrees with the spline in pp on the rectangle [b4 .. b5] x [-1 .. 1] , where b4, b5 are the fourth and fifth entry in the break sequence for the first variable.

See Also

ppalldem, ppmak, rsmak, spalldem, spmak, stmak

fn2fm

fncmb