Spline Toolbox

Constructive vs. Variational

The above constructive approach is not the only avenue to splines. In the variational approach, a spline is obtained as a best interpolant, e.g., as the function with smallest 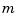th derivative among all those matching prescribed function values at certain sites. As it turns out, among the many such splines available, only those that are piecewise-polynomials or, perhaps, piecewise- exponentials have found much use. 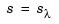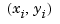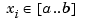Of particular practical interest is the smoothing spline which, for given data with , all 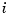, and given corresponding positive weights 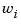, and for given smoothing parameter 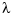, minimizes

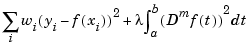
over all functions 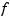with 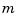derivatives. It turns out that the smoothing spline 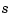is a spline of order 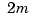with a break at every data site. The art of using the smoothing spline consists in choosing 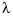so that 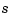contains as much of the information, and as little of the supposed noise, in the data as possible.

B-Spline Properties

Multivariate Splines