| Spline Toolbox | |
Multivariate Splines
Multivariate splines can be obtained from univariate splines by the tensor product construct. For example, a trivariate spline in B-form is given by
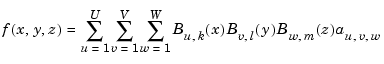
with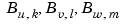 
univariate B-splines. Correspondingly, this spline is of order 
in 
, of order 
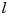in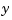 
, and of order 
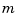in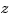 
. Similarly, the ppform of a tensor-product spline is specified by break sequences in each of the variables and, for each hyper-rectangle thereby specified, a coefficient array. Further, as in the univariate case, the coefficients may be vectors, typically 2-vectors or 3-vectors, making it possible to represent, e.g., certain surfaces in R3.
A very different bivariate spline is the thin-plate spline. This is a function of the form
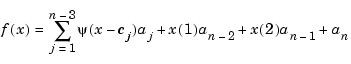
with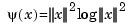 
the thin-plate spline basis function, and 
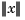denoting the Euclidean length of the vector 
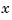. Here, for convenience, we denote the independent variable by 
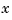, but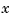 
is now a vector whose two components, 
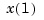and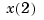 
, play the role of the two independent variables earlier denoted 
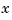and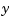 
. Correspondingly, the sites 
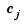are points in 
.
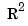Thin-plate splines arise as bivariate smoothing splines, meaning a thin-plate spline minimizes
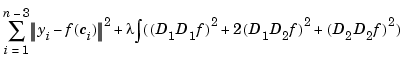
over all sufficiently smooth functions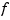 
. Here, the 
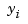are data values given at the data sites 
, 
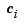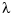is the smoothing parameter, and 
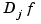denotes the partial derivative of 
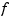with respect to 
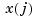. The integral is taken over the entire 
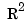. The upper summation limit, 
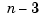, reflects the fact that 3 degrees of freedom of the thin-plate spline are associated with its polynomial part.
Thin-plate splines are functions in stform, meaning that, up to certain polynomial terms, they are a weighted sum of arbitrary or scattered translates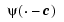 
of one fixed function, 
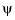. This so-called basis function for the thin-plate spline is special in that it is radially symmetric, meaning that 
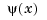only depends on the Euclidean length, 
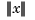, of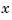 
. For that reason, thin-plate splines are also known as RBFs or radial basis functions. See The stform for more information.
| | Constructive vs. Variational | The ppform | |