Spline Toolbox

B-Spline Properties

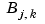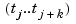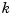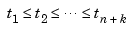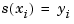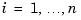Since is nonzero only on the interval , the linear system for the B-spline coefficients of the spline to be determined, by interpolation or least squares approximation, or even as the approximate solution of some differential equation, is banded, making the solving of that linear system particularly easy. For example, if a spline s of order with knot sequence is to be constructed so that for , then we are led to the linear system

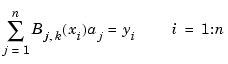
for the unknown B-spline coefficients 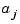in which each equation has at most 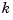nonzero entries.

Also, many theoretical facts concerning splines are most easily stated and/or proved in terms of B-splines. For example, it is possible to match arbitrary data at sites 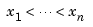uniquely by a spline of order 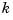with knot sequence 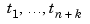if and only if 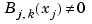for all 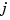(Schoenberg-Whitney Conditions). Computations with B-splines are facilitated by stable recurrence relations

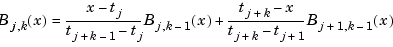
that are also of help in the conversion from B-form to ppform. The dual functional   

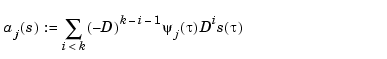
provides a useful expression for the jth B-spline coefficient of the spline s in terms of its value and derivatives at an arbitrary site 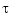between 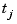and 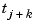, and with

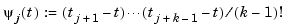. It can be used to show that 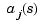is closely related to 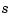on the interval 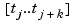, and seems the most efficient means for converting from ppform to B-form.

Knot Multiplicity

Constructive vs. Variational