

| Spline Toolbox |   |
Knot distribution "optimal" for interpolation
Syntax
Description
t= optknt(tau,k,maxiter)
t that is best for interpolation from 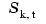 at the site sequence
at the site sequence tau, with 10 the default for the optional input maxiter that bounds the number of iterations to be used in this effort. Here, best or optimal is used in the sense of [3] and [2], and this means the following: For any recovery scheme 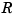 that provides an interpolant
that provides an interpolant 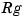 that matches a given
that matches a given 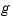 at the sites
at the sites tau(1), ..., tau(n), we may determine the smallest constant 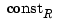 for which
for which
 for all smooth functions
for all smooth functions 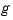 .
.
Here,
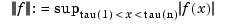 . Then we may look for the optimal recovery scheme as the scheme
. Then we may look for the optimal recovery scheme as the scheme 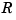 for which
for which  is as small as possible. Micchelli/Rivlin/Winograd have shown this to be interpolation from
is as small as possible. Micchelli/Rivlin/Winograd have shown this to be interpolation from 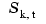 , with
, with t uniquely determined by the following conditions:
t(1) = ... = t(k) = tau(1);
t(n+1) = ... = t(n+k) = tau(n);
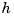 with sign changes at the sites
with sign changes at the sites t(k+1), ..., t(n) and nowhere else satisfies
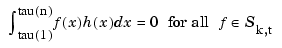
Gaffney/Powell called this interpolation scheme optimal since it provides the center function in the band formed by all interpolants to the given data that, in addition, have their 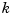 th derivative between
th derivative between 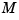 and
and 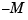 (for large
(for large 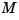 ).
).
Examples
See the last part of the demo spapidem for an illustration. For the following highly nonuniform knot sequence
the command optknt(t,3) will fail, while the command optknt(t,3,20), using a high value for the optional parameter maxiter, will succeed.
Algorithm
This is the Fortran routine SPLOPT in PGS. It is based on an algorithm described in [1], for the construction of that sign function 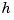 mentioned in (3) above. It is essentially Newton's method for the solution of the resulting nonlinear system of equations, with
mentioned in (3) above. It is essentially Newton's method for the solution of the resulting nonlinear system of equations, with aveknt(tau,k) providing the first guess for t(k+1), ...,t(n), and some damping used to maintain the Schoenberg-Whitney conditions .
See Also
aptknt, aveknt, newknt, spapidem
References
[1] C. de Boor, "Computational aspects of optimal recovery", in Optimal Estimation in Approximation Theory, C.A. Micchelli & T.J. Rivlin eds., Plenum Publ., New York, 1977, 69-91.
[2] P.W. Gaffney & M.J.D. Powell, "Optimal interpolation", in Numerical Analysis, G.A. Watson ed., Lecture Notes in Mathematics, No. 506, Springer-Verlag, 1976, 90-99.
[3] C.A. Micchelli, T.J. Rivlin & S. Winograd, "The optimal recovery of smooth functions", Numer. Math. 80, (1974), 903-906.
 | newknt | ppmak |  |