| Spline Toolbox | |
Syntax
Description
newknt(f,newl)
f into newl pieces, in such a way that a certain piecewise linear monotone function related to the high derivative of f is equidistributed.
The intent is to choose a knot sequence suitable to the fine approximation of a
function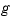 
whose rough approximation in f is assumed to contain enough
information about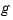 
to make this feasible.
newknt(f)
uses for newl its default value, namely the number of polynomial pieces in f.
[newknots,distfn]=newknt(f,...)
also returns the ppform of that piecewise linear monotone function being equidistributed.
Examples
If the error in the least-squares approximation sp to some data x,y by a spline of order k seems uneven, you might try for a more equitable distribution of knots by using
For another example, see the last part of the demo difeqdem.
Algorithm
This is the Fortran routine NEWNOT in PGS. With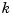 
the order of the piecewise-polynomial function 
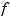in pp, the function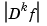 
is approximated by a piecewise constant function obtained by local, discrete, differentiation of the variation of 
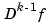. The new break sequence is chosen to subdivide the basic interval of the piecewise-polynomial 
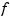in such a way that
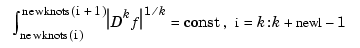
See Also
| | knt2brk, knt2mlt | optknt | |