| Partial Differential Equation Toolbox | |
Syntax
[cgxu,cgyu]=pdecgrad(p,t,c,u) [cgxu,cgyu]=pdecgrad(p,t,c,u,time) [cgxu,cgyu]=pdecgrad(p,t,c,u,time,sdl)
Description
[cgxu,cgyu]=pdecgrad(p,t,c,u)
returns the flux, c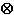 
u, evaluated at the center of each triangle.
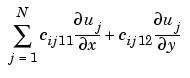
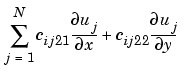
There is one column for each triangle in t in both cgxu and cgyu.
The geometry of the PDE problem is given by the mesh data p and t. Details on the mesh data representation can be found in the entry on initmesh.
The coefficient c of the PDE problem can be given in a variety of ways. A complete listing of all options can be found in the entry on assempde.
The format for the solution vector u is described in assempde.
The scalar optional argument time is used for parabolic and hyperbolic problems, if c depends on t, the time.
The optional argument sdl restricts the computation to the subdomains in the list sdl.
See Also
| | pdebound | pdecirc | |