| Model Predictive Control Toolbox | |
Model predictive controller for simulating closed-loop systems with hard bounds on manipulated variables and/or controlled variables using linear models in the MPC step format for nonlinear plants represented as Simulink S-functions.
Description
nlcmpc is a Simulink S-function block and can be invoked by typing nlmpclib at the MATLAB prompt. Its usage is identical to other Simulink blocks. The input to nlcmpc includes both the variables controlled by nlcmpc and measured disturbances. The first ny elements of the input are treated as the controlled variables while the rest is taken as the measured disturbances. The output from nlcmpc are the values of the manipulated variables. Initial conditions for the manipulated variables and the measured disturbances must be specified. The controlled variables sent to nlcmpc and the manipulated variables returned by nlcmpc are actual variables; they are not deviation variables.
Because of the limit on the number of masked variables that can be specified for a Simulink block, model and dmodel are put together as "one" variable, r, ywt, and uwt as "one" variable, and ylim and ulim as "one" variable. m and p should be entered as one row vector. u0 and d0 should also be entered as one row vector. The required input variables are as follows:
modelpd
Equals [model dmodel]. model is a linear model in the MPC step format that is to be used for state estimation in the controller. In general, it is a linear approximation of the nonlinear plant. dmodel is a model in MPC step format representing the effect of the measured disturbances. The default is no measured disturbances. Note that the truncation time for model and dmodel must be the same and the number of outputs for model and dmodel must be the same.
ryuwt
Equals [r ywt uwt]. r is a setpoint matrix consisting of N rows and ny columns, where ny is the number of output variables, y:
Where ri(k) is the setpoint for output i at time t = kT, and T is the sampling period (as specified in the step format of model). If the simulation time is larger than NT, the setpoints vary for the first N periods in the simulation, as specified by r, and are then held constant at the values given in the last row of r for the remainder of the simulation. In many simulations one wants the setpoints to be constant for the entire time, in which case r need only contain a single row of ny values.
ywt
Must have ny columns, where ny is the number of outputs. All weights must be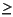 
0.
You may vary the weights at each step in the prediction horizon by including up to P rows in ywt. Then the first row of ny values applies to the tracking errors in the first step in the prediction horizon, the next row applies to the next step, etc. See mpccon for details on the form of the optimization objective function.
If you supply only nrow rows, where 1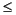 
nrow < P, nlcmpc will use the last row to fill in any remaining steps. Thus if you wish the weighting to be the same for all P steps, you need only specify a single row.
uwt
Has the same format as ywt, except that uwt applies to the changes in the manipulated variables. If uwt, it must have nu columns, where nu is the number of manipulated variables.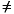
[ ]
Notice that the number of rows for r, ywt, and uwt should be the same. If not, one can enter the variable as parpart(r, ywt, uwt). The function parpart appends extra rows to r, ywt, and/or uwt so that they have the same number of rows. The default is r=y0, where y0 is the initial condition for the output, equal (unity) weighting of all outputs over the entire prediction horizon and zero weighting of all input.
mp
Equals [M P]. P equals the last element of MP. There are two ways to specify M: If it is a scalar, nlcmpc interprets it as the input horizon (number of moves) as in DMC; if it is a row vector containing nb elements, each element of the vector indicates number of the steps over which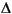 
u(k) = 0 during the optimization and nlcmpc interprets it as a set of nb blocking factors. There may be 1 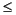nb 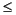P blocking factors, and their sum must be 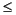P. If you set M=[ ], the default is M = P, which is equivalent to M=ones(1,P). P is the number of sampling periods in the prediction horizon.
yulim
Equals [ylim ulim]. ulim is a matrix giving the limits on the manipulated variables. Its format is as follows:
Note that it contains three matrices of N rows. In this case, the limits on N are 1 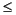N 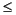nb, where nb is the number of times the manipulated variables are to change over the input horizon. If you supply fewer than nb rows, the last row is repeated automatically.
The first matrix specifies the lower bounds on the nu manipulated variables. For example, umin,j(2) is the lower bound for manipulated variable j for the second move of the manipulated variables (where the first move is at the start of the prediction horizon). If umin,j(k) = -inf, manipulated variable j will have no lower bound for that move.
The second matrix gives the upper bounds on the manipulated variables. If umax,j(k) = inf, manipulated variable j will have no upper bound for that move.
The lower and upper bounds may be either positive or negative (or zero) as long as umin,j(k) 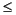umax,j(k).
The third matrix gives the limits on the rate of change of the manipulated variables. In other words, cmpc will force|uj(k) - uj(k - 1)| 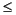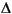umax,j(k). The limits on the rate of change must be nonnegative and finite. If you want it to be unbounded, set the bound to a large number (but not too large -- a value of 106 should work well in most cases).
ylim has the same format as ulim, but for the lower and upper bounds of the outputs. The first row applies to the first point in the prediction horizon.
Note that the number of rows for ylim and ulim should be the same. If the number of rows for ylim and ulim differs, one can use parpart(ylim, ulim). The function parpart appends extra rows to ylim or ulim so that they have the same number of rows. If you set yulim = [ ], then umin = -inf, umax = inf, umax = 106, ymin = -inf and ymax = inf.
tfilter
Is a matrix of time constants for the noise filter and the unmeasured disturbances entering at the plant output. The first row of ny elements gives the noise filter time constants and the second row of ny elements gives the time constants of the lags through which the unmeasured disturbance steps pass. If tfilter only contains one row, the unmeasured disturbances are assumed to be steps. If you set tfilter= [ ], no noise filtering and steplike unmeasured disturbances are assumed.
ud0
Equals [u0 d0]. u0 are initial values of the manipulated variables arranged in a row vector having nu elements; nu is the number of the manipulated variables computed by nlcmpc. d0 are initial values of the measured disturbances arranged in a row vector having nd elements; nd is the number of the measured disturbances. The default is u0 = 0 and d0 = 0.
Notes
nlcmpc are specified through nlcmpc while initial conditions for the controlled variables are specified through the S-function for the nonlinear plant.
r, ulim and ylim, should that be appropriate for your simulation.
ulim constraints used here are fundamentally different from the usat constraints used in the nlmpcsim block. The ulim constraints are defined relative to the beginning of the prediction horizon, which moves as the simulation progresses. Thus at each sampling period, k, the ulim constraints apply to a block of calculated moves that begin at sampling period k and extend for the duration of the input horizon. The usat constraints, on the other hand, are relative to the fixed point t = 0, the start of the simulation.
nlcmpc and nlmpcsim should give the same results. The latter will be faster because it uses an analytical solution of the QP problem, whereas nlcmpc solves it by iteration.
Example
See the examples for nlmpcsim with one modification: replace the block nlmpcsim with nlcmpc. Clearly, additional variables should be defined appropriately.
| mpcsim | nlmpcsim | |