Model Predictive Control Toolbox

Calculates the complex frequency response in varying format of a system in MPC mod format.

Syntax

• frsp = mod2frsp(mod,freq)
  [frsp,eyefrsp] = mod2frsp(mod,freq,out,in,balflg) 
  

Description
mod2frsp calculates the complex frequency response of a system (mod) in MPC mod format. The desired frequencies are given by the input freq, a row vector of 3 elements specifying the lower frequency as a power of 10, the upper frequency as a power of 10, and the number of frequency points.

Optional inputs out and in are row vectors that specify the outputs and inputs for which the frequency response is to be generated. If these variables are omitted or empty, the default is to use all outputs and inputs.

Optional input balflg indicates whether the system's 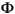matrix should be balanced (using the MATLAB balance command). If balflg is nonzero, balancing is performed. Balancing improves the conditioning of the problem, but may cause errors in the frequency response. If balflg=[ ] or is omitted, no balancing is performed.

Output frsp is the frequency response matrix given in varying format. Let F(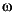) denote a matrix-valued function of the independent variable 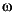. Then the N sampled values F(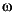₁), . . . , F(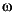N) are contained in frsp as follows:

If the dimension of each submatrix F(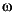i) is n by m, then the dimensions of frsp is n . N + 1 by m + 1.

Optional output eyefrsp is in varying format and represents I - F(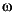i) at each frequency. This output can only be specified for square submatrices and may be useful in computing the frequency responses of both the sensitivity and complementary sensitivity functions.

Example
Consider the linear system:

See the mpccl example for the commands that build the a closed-loop model for this process using a simple controller. However for this example, delt=6 and tfinal=90 are used to reduce the number of step response coefficients.

Now we will calculate and plot the frequency response of the sensitivity and complementary sensitivity functions.

• freq = [-3,0,30]; 
  in = [1:ny]; % input is r for comp. sensitivity 
  out = [1:ny]; % output is yp for comp. sensitivity 
  [frsp,eyefrsp] = mod2frsp(clmod,freq,out,in); 
  plotfrsp(eyefrsp); % Sensitivity 
  pause;
  
  
  plotfrsp(frsp); % Complementary Sensitivity pause;
  
  
  

• [sigma,omega] = svdfrsp(eyefrsp);
  clg;
  semilogx(omega,sigma);
  title('Singular Values vs. Frequency');
  xlabel('Frequency (radians/time)');
  ylabel('Singular Values');
  
  
  

Algorithm
The algorithm to calculate the complex frequency response involves a matrix inverse problem which is solved via a Hessenberg matrix.

Reference
A.J. Laub, "Efficient Multivariable Frequency Response Computations," IEEE Transactions on Automatic Control, Vol. AC-26, No. 2, pp.407-408, April, 1981.

See Also
mod, mpccl, plotfrsp, smpccl, svdfrsp

mod format

mod2mod