

| Model Browser User's Guide |   |
Global Models
Modeling the variation in the response features as a function of the global variables. The response features are carried through to the second stage of the modeling procedure rather than the curve fit parameters because they have an engineering interpretation. This ensures that the second stage of the modeling process remains relatively intuitive. It is much more likely that an engineer will have better knowledge of how a response feature such as MBT behaves throughout the engine operating range (at least on a main effects basis) as opposed to an esoteric curve fit parameter estimate.
The global relationship is represented by one of the global models available in the Model-Based Calibration Toolbox. In this section we only consider linear models that can be represented as
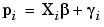 for for 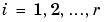
|
(6-9) |
where the Xi contains the information about the engine operating conditions at the ith spark sweep, 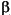 is the vector of global parameter estimates that must be estimated by the fitting procedure, and
is the vector of global parameter estimates that must be estimated by the fitting procedure, and 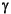 i is a vector of normally distributed random errors. It is necessary to make some assumption about the error distribution for
i is a vector of normally distributed random errors. It is necessary to make some assumption about the error distribution for 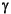 , and this is typically a normal distribution with
, and this is typically a normal distribution with
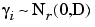
|
(6-10) |
where r is the number of response features. The dimensions of D are (rxr) and, being a variance-covariance matrix, D is both symmetric and positive definite. Terms on the leading diagonal of D represent the test-to-test variance associated with the estimate of the individual response features. Off-diagonal terms represent the covariance between pairs of response features. The estimation of these additional covariance terms in a multivariate analysis improves the precision of the parameter estimates.
 | Local Models | Two-Stage Models |  |