

| Model Browser User's Guide |   |
Local Models
Modeling responses locally within a sweep as a function of the independent variable only. That is,
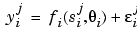 for for 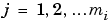
|
(6-1) |
where the subscript i refers to individual tests and j to data within a test, 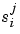 is the jth independent value,
is the jth independent value, 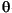 i is a (rx1) parameter vector,
i is a (rx1) parameter vector, 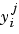 is the j th response, and
is the j th response, and 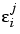 is a normally distributed random variable with zero mean and variance
is a normally distributed random variable with zero mean and variance 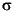 2. Note that Equation 6-1 can be either a linear or a nonlinear function of the curve fit parameters. The assumption of independently normally distributed errors implies that the least squares estimates of
2. Note that Equation 6-1 can be either a linear or a nonlinear function of the curve fit parameters. The assumption of independently normally distributed errors implies that the least squares estimates of 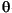 are also maximum likelihood parameters.
are also maximum likelihood parameters.
Local Covariance Modeling
The local model describes both the systematic and random variation associated with measurements taken during the ith test. Systematic variation is characterized through the function f while variation is characterized via the distributional assumptions made on the vector of random errors ei. Hence, specification of a model for the distribution of ei completes the description of the intratest model. The Model-Based Calibration Toolbox allows a very general specification of the local covariance,
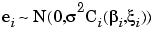
|
(6-2) |
where Ci is an (ni x ni) covariance matrix, 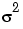 is the coefficient of variation, and
is the coefficient of variation, and 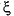 i is a (q-by-1) vector of dispersion parameters that account for heterogeneity of variance and the possibility of serially correlated data. The specification is very general and affords considerable flexibility in terms of specifying a covariance model to adequately describe the random component of the intratest variation.
i is a (q-by-1) vector of dispersion parameters that account for heterogeneity of variance and the possibility of serially correlated data. The specification is very general and affords considerable flexibility in terms of specifying a covariance model to adequately describe the random component of the intratest variation.
The Model-Based Calibration Toolbox supports the following covariance models:
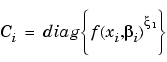
|
(6-3) |
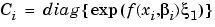
|
(6-4) |
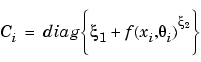
|
(6-5) |
where diag{x} is a diagonal matrix.
Correlation models are only available for equispaced data in the Model-Based Calibration Toolbox. It is possible to combine correlation models with models with the variance models such as power.
One of the simplest structures that can be used to account for serially correlated errors is the AR(m) model (autoregressive model with lag m). The general form of the AR(m) model is
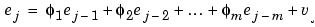
|
(6-6) |
where 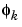 is the kth lag coefficient and vj is an exogenous stochastic input identically and independently distributed as
is the kth lag coefficient and vj is an exogenous stochastic input identically and independently distributed as 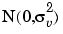 . First- and second-order autoregressive models are implemented in the Model-Based Calibration Toolbox.
. First- and second-order autoregressive models are implemented in the Model-Based Calibration Toolbox.
Another possibility is a moving average model (MA). The general structure is
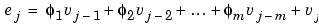
|
(6-7) |
where 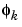 is the kth lag coefficient and vj is an exogenous stochastic input identically and independently distributed as
is the kth lag coefficient and vj is an exogenous stochastic input identically and independently distributed as 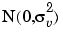 . Only a first-order moving average model is implemented in the Model-Based Calibration Toolbox.
. Only a first-order moving average model is implemented in the Model-Based Calibration Toolbox.
Response Features
From an engineering perspective, the curve fit parameters do not usually have any intuitive interpretation. Rather characteristic geometric features of the curve are of interest. The terminology "response features" of Crowder and Hand [7] is used to describe these geometric features of interest. In general, the response feature vector pi for the ith sweep is a nonlinear function (g) of the corresponding curve fit parameter vector 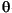 i, such that
i, such that
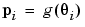
|
(6-8) |
 | Two-Stage Models for Engines | Global Models |  |