GARCH Toolbox

Forecasting Using a Regression Component

Inclusion of a regression component in forecasting is also similar to including one in an estimation. However, in addition to the explanatory data, you must consider the use of forecasted explanatory data.

This section discusses:

• Forecasted Explanatory Data
• Generating the Forecasted Explanatory Data
• Ordinary Least Squares Regression

Forecasted Explanatory Data

If you want to forecast the conditional mean of a return series y in each period of a 10-period forecast horizon, the correct calling syntax for garchpred is

• [sFcast, yFcast] = garchpred(spec, y, 10, X, XF);
  

where X is the same regression matrix shown above, and XF is a regression matrix of forecasted explanatory data. In fact, XF represents a projection into the future of the same explanatory data found in X. Note that the command above produces an error if you execute it in your current workspace because XF is missing.

XF must have the same number of columns as X. In each column of XF, the first row contains the one-period-ahead forecast, the second row the two-period-ahead forecast, and so on. If you specify XF, the number of rows (forecasts) in each column of must equal or exceed the forecast horizon. When the number of forecasts in XF exceeds the 10-period forecast horizon, garchpred uses only the first 10 forecasts. If XF is empty ([]) or missing, the conditional mean forecast has no regression component.

You should use the same regression matrix X when calling garchpred that you used for simulation and/or estimation. This is because garchpred requires a complete conditional mean specification to correctly infer the innovations {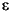_t} from the observed return series {y_t}.

Forecasting the Conditional Standard Deviation.   If you only need to forecast the conditional standard deviation (i.e., sFcast), XF is unnecessary. This is true even if you included the matrix X in the simulation and/or estimation process.

For example, you would use the following syntax to forecast only the conditional standard deviation of the return series y over a 10-period forecast horizon

• sFcast = garchpred(spec, y, 10, X);
  

Forecasting the Conditional Mean.   If you specify X, you must also specify XF to forecast the conditional mean (i.e., yFcast).

For example, to forecast the conditional mean of the return series y over a 10-period forecast horizon,

• [sFcast yFcast] = garchpred(spec, y, 10, X, XF);
  

The forecasted explanatory data, XF, does not affect the standard deviation forecast. Note that this command produces an error if you execute it in your current workspace because XF is missing.

Generating the Forecasted Explanatory Data

Typically, the regression matrix X contains the observed returns of a suitable market index, collected over the same time interval as the observed data of interest. In this case, X is most likely a vector, corresponding to a single explanatory variable, and you must devise some way of generating the forecast of X (i.e., XF).

One approach, using the GARCH Toolbox, is to first use garchfit to fit a suitable ARMA(R,M) model to the returns in X, then use garchpred to forecast the market index returns into the future. Specifically, since you're not interested in fitting the volatility of X, you can simplify the estimation process by assuming a constant conditional variance model, i.e. ARMA(R,M)/GARCH(0,0).

Ordinary Least Squares Regression

The following example illustrates an ordinary least squares regression by simulating a return series that scales the returns of the XYZ Corporation. It also provides an example of a constant conditional variance model. A model like this might, for example, represent a leveraged position in the common stock of the XYZ Corporation.

First, create a specification structure. Set the Display flag to off to suppress the optimization details that garchfit normally prints to the screen.

• spec = garchset('Display', 'off');
  spec = garchset(spec, 'P', 0, 'Q', 0);
  spec = garchset(spec, 'C', 0, 'Regress', 1.2, 'K', 0.00015)
  spec = 
           Comment: 'Mean: ARMAX(0,0,?); Variance: GARCH(0,0)'
                 R: 0
                 M: 0
                 P: 0
                 Q: 0
      Distribution: 'Gaussian'
                 C: 0
                AR: []
                MA: []
           Regress: 1.2000
                 K: 1.5000e-004
             GARCH: []
              ARCH: []
              FixC: []
             FixAR: []
             FixMA: []
        FixRegress: []
              FixK: []
          FixGARCH: []
           FixARCH: []
      Optimization: [1x1 struct]
  

Now, simulate a single realization of 2000 observations, fit the model, and examine the results

• [e, s, y] = garchsim(spec, 2000, 1, [], xyz);
  [coeff, errors] = garchfit(spec, y, xyz);
  garchdisp(coeff, errors)
   
    Number of Parameters Estimated: 3
  
                                 Standard          T     
    Parameter       Value          Error       Statistic 
   -----------   -----------   ------------   -----------
            C    -5.5043e-006   0.0002711       -0.0203
   Regress(1)    1.2402         0.020454        60.6304
            K    0.0001464      4.6871e-006     31.2345
  

These estimation results are just the ordinary least squares (OLS) regression results. In fact, in the absence of GARCH effects and assuming Gaussian innovations, maximum likelihood estimation and least squares regression are the same thing.

Note    This example is shown purely for illustration purposes. Although you can use the GARCH Toolbox to perform OLS, it is computationally inefficient and is not recommended.

Simulation and Inference Using a Regression Component

Regression in a Monte Carlo Framework