| GARCH Toolbox | |
Parameter Estimation
Estimate the Model Parameters
The presence of heteroscedasticity, shown in the previous analysis, indicates that GARCH modeling is appropriate. Use the estimation function garchfit to estimate the model parameters. Assume the default GARCH model described in the section The Default Model. This only requires that you specify the return series of interest as an argument to the function garchfit.
Note
Because the default value of the Display parameter in the specification structure is on, garchfit prints diagnostic, optimization, and summary information to the MATLAB command window in the example below. (See fmincon in the Optimization Toolbox for information about the optimization information.)
|
[coeff, errors, LLF, innovations, sigma, summary] = garchfit(xyz); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Diagnostic Information Number of variables: 4 Functions Objective: garchllfn Gradient: finite-differencing Hessian: finite-differencing (or Quasi-Newton) Nonlinear constraints: garchnlc Gradient of nonlinear constraints: finite-differencing Constraints Number of nonlinear inequality constraints: 0 Number of nonlinear equality constraints: 0 Number of linear inequality constraints: 1 Number of linear equality constraints: 0 Number of lower bound constraints: 4 Number of upper bound constraints: 0 Algorithm selected medium-scale %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% End diagnostic information max Directional Iter F-count f(x) constraint Step-size derivative Procedure 1 5 -5921.94 -1.684e-005 1 -7.92e+004 2 34 -5921.94 -1.684e-005 1.19e-007 -553 3 43 -5924.42 -1.474e-005 0.125 -31.2 4 49 -5936.16 -6.996e-021 1 -288 5 57 -5960.62 0 0.25 -649 6 68 -5961.45 -4.723e-006 0.0313 -17.3 7 75 -5963.18 -2.361e-006 0.5 -28.6 8 81 -5968.24 0 1 -55 9 90 -5970.54 -6.016e-007 0.125 -196 10 103 -5970.84 -1.244e-006 0.00781 -16.1 11 110 -5972.77 -9.096e-007 0.5 -34.4 12 126 -5972.77 -9.354e-007 0.000977 -24.5 13 134 -5973.29 -1.05e-006 0.25 -4.97 14 141 -5973.95 -6.234e-007 0.5 -1.99 15 147 -5974.21 -1.002e-006 1 -0.641 16 153 -5974.57 -9.028e-007 1 -0.0803 17 159 -5974.59 -8.054e-007 1 -0.0293 18 165 -5974.6 -8.305e-007 1 -0.0039 19 172 -5974.6 -8.355e-007 0.5 -0.000964 20 192 -5974.6 -8.355e-007 -6.1e-005 -0.000646 21 212 -5974.6 -8.355e-007 -6.1e-005 -0.000996 Hessian modified twice 22 219 -5974.6 -8.361e-007 0.5 -0.000184 23 239 -5974.6 -8.361e-007 -6.1e-005 -0.00441 Hessian modified twice Optimization terminated successfully: Search direction less than 2*options.TolX and maximum constraint violation is less than options.TolCon No Active Constraints
Examine the Estimated GARCH Model
Now that the estimation is complete, you can display the parameter estimates and their standard errors using the function garchdisp,
garchdisp(coeff, errors) Number of Parameters Estimated: 4 Standard T Parameter Value Error Statistic ----------- ----------- ------------ ----------- C 0.00049183 0.00025585 1.9223 K 8.2736e-007 2.7446e-007 3.0145 GARCH(1) 0.96283 0.0051557 186.7500 ARCH(1) 0.03178 0.004416 7.1965
If you substitute these estimates in the definition of the default model, Eq. (2-12) and Eq. (2-13), the estimation process implies that the constant conditional mean/GARCH(1,1) conditional variance model that best fits the observed data is
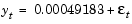
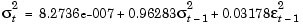
where G1 = GARCH(1) = 0.96283 and A1 = ARCH(1) = 0.03178. In addition, C = C = 0.00049183 and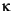 
= K = 8.2736e-007.
Figure 2-10, GARCH(1,1) Log-Likelihood Contours for the XYZ Corporation shows the log-likelihood contours of the default GARCH(1,1) model fit to the returns of the XYZ Corporation. The contour data is generated by the GARCH Toolbox demonstration function garch11grid. This function evaluates the log-likelihood function on a grid in the G1-A1 plane, holding the parameters C and 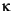fixed at their maximum likelihood estimates of 0.00049183 and 8.2736e-007, respectively.
The contours confirm the printed garchfit results above. The maximum log-likelihood value, LLF = 5974.6, occurs at the coordinates G1 = GARCH(1) = 0.96283 and A1 = ARCH(1) = 0.03178.
The figure also reveals a highly negative correlation between the estimates of the G1 and A1 parameters of the GARCH(1,1) model. This implies that a small change in the estimate of the G1 parameter is nearly compensated for by a corresponding change of opposite sign in the A1 parameter.
Figure 2-10: GARCH(1,1) Log-Likelihood Contours for the XYZ Corporation
| Note If you view this manual on the Web, the color-coded bar at the right of the figure indicates the height of the log-likelihood surface above the GARCH(1,1) plane. |
| | Pre-Estimation Analysis | Post-Estimation Analysis | |
