GARCH Toolbox

lbqtest

Ljung-Box Q-statistic lack-of-fit hypothesis test

Syntax

• [H, pValue, Qstat, CriticalValue] = lbqtest(Series, Lags, Alpha, 
  DoF)
  

Arguments

Series	Vector of observations of a univariate time series for which lbqtest computes the sample Q-statistic. The last row of Series contains the most recent observation of the stochastic sequence. Typically, Series is either the sample residuals derived from fitting a model to an observed time series, or the standardized residuals obtained by dividing the sample residuals by the conditional standard deviations.
Lags	(optional) Vector of positive integers indicating the lags of the sample autocorrelation function included in the Q-statistic. If specified, each lag must be less than the length of Series. If Lags = [] or is not specified, the default is Lags = min([20, length(Series)-1]).
Alpha	(optional) Significance level(s). Alpha can be a scalar applied to all lags, or a vector the same length as Lags. If Alpha = [] or is not specified, the default is 0.05. For all elements, 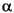, of Alpha, 0 < 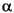 < 1.
DoF	(optional) Degree(s) of freedom. DoF can be a scalar applied to all lags, or a vector the same length as Lags. If specified, all elements of DoF must be positive integers less than the corresponding element of Lags. If DoF = [] or is not specified, the elements of Lags serve as the default degrees of freedom for the Chi-Square distribution.

Description

[H, pValue, Qstat, CriticalValue] = lbqtest(Series, Lags, Alpha, DoF) performs the Ljung-Box lack-of-fit hypothesis test for model misspecification, which is based on the Q-statistic

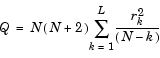
where N = sample size, L = number of autocorrelation lags included in the statistic, and r_k² is the squared sample autocorrelation at lag k. Once you fit a univariate model to an observed time series, you can use the Q-statistic as a lack-of-fit test for a departure from randomness. Under the null hypothesis that the model fit is adequate, the test statistic is asymptotically Chi-Square distributed.

H	Boolean decision vector. 0 indicates acceptance of the null hypothesis that the model fit is adequate (no serial correlation at the corresponding element of Lags). 1 indicates rejection of the null hypothesis. H is the same size as Lags.
pValue	Vector of P-values (significance levels) at which lbqtest rejects the null hypothesis of no serial correlation at each lag in Lags.
Qstat	Vector of Q-statistics for each lag in Lags.
CriticalValue	Vector of critical values of the Chi-Square distribution for comparison with the corresponding element of Qstat.

Example

Create a vector of 100 Gaussian random numbers, then compute the Q-statistic for autocorrelation lags 20 and 25 at the 10 percent significance level.

• randn('state',100)               % Start from a known state.
  Series         = randn(100,1);   % 100 Gaussian deviates ~ N(0,1)
  [H,P,Qstat,CV] = lbqtest(Series, [20 25]', 0.10);
  [H,P,Qstat,CV]
  
  ans =
  
           0    0.9615   10.3416   28.4120
           0    0.9857   12.1015   34.3816
  

See Also
archtest, autocorr

Reference

[1]  Box, G.E.P., G.M. Jenkins, G.C. Reinsel, Time Series Analysis: Forecasting and Control, third edition, Prentice Hall, 1994.

[2]  Gourieroux, C., ARCH Models and Financial Applications, Springer-Verlag, 1997.

lagmatrix

lratiotest