Financial Derivatives Toolbox

Heath-Jarrow-Morton (HJM) Model

The Heath-Jarrow-Morton (HJM) model is one of the most widely used models for pricing interest rate derivatives. The model considers a given initial term structure of interest rates and a specification of the volatility of forward rates to build a tree representing the evolution of the interest rates, based upon a statistical process. For further explanation, see the book "Modelling Fixed Income Securities and Interest Rate Options" by Robert A. Jarrow.

Building an HJM Forward Rate Tree

The HJM tree of forward rates is the fundamental unit representing the evolution of interest rates in a given period of time. This section explains how to create the HJM forward rate tree using the Financial Derivatives Toolbox.

The MATLAB function that creates the HJM forward rate tree is hjmtree. This function takes three structures as input arguments:

• The volatility model VolSpec. (See Specifying the Volatility Model (VolSpec).)
• The interest rate term structure RateSpec. (See Specifying the Interest Rate Term Structure (RateSpec).)
• The tree time layout TimeSpec. (See Specifying the Time Structure (TimeSpec).)

Creating the HJM Forward Rate Tree (hjmtree)

Calling the function hjmtree creates the structure, HJMTree, containing time and forward rate information for a bushy tree.

This structure is a self-contained unit that includes the HJM tree of rates (found in the FwdTree field of the structure), and the volatility, rate, and time specifications used in building this tree.

The calling syntax for hjmtree is

• HJMTree = hjmtree(VolSpec, RateSpec, TimeSpec)
  

where:

• VolSpec is a structure that specifies the forward rate volatility process. VolSpec is created using the function hjmvolspec. The hjmvolspec function supports the specification of multiple factors. It handles five models for the volatility of the interest rate term structure:
• Constant
• Stationary
• Exponential
• Vasicek
• Proportional

• Incorporating multiple factors allows you to specify different types of shifts in the shape and location of the interest rate structure. A one-factor model assumes that the interest term structure is affected by a single source of uncertainty.

• RateSpec is the interest rate specification of the initial rate curve. This structure is created with the function intenvset. (See Interest Rate Term Structure.)
• TimeSpec is the tree time layout specification. This variable is created with the function hjmtimespec. It represents the mapping between level times and level dates for rate quoting. This structure determines indirectly the number of levels of the tree generated in the call to hjmtree.

Specifying the Volatility Model (VolSpec)

The function hjmvolspec generates the structure VolSpec, which specifies the volatility process 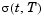used in the creation of the forward rate trees. In this context 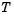represents the starting time of the forward rate, and 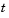represents the observation time. The volatility process can be constructed from a combination of factors specified sequentially in the call to hjmvolspec. Each factor specification starts with a string specifying the name of the factor, followed by the pertinent parameters.

Consider an example that uses a single factor, specifically, a constant-sigma factor. The constant factor specification requires only one parameter, the value of 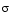. In this case, the value corresponds to 0.10.

• VolSpec = hjmvolspec('Constant', 0.10)
  
  VolSpec = 
  
        FinObj: 'HJMVolSpec'
  FactorModels: {'Constant'}
    FactorArgs: {{1x1 cell}}
    SigmaShift: 0
    NumFactors: 1
     NumBranch: 2
       PBranch: [0.5000 0.5000]
   Fact2Branch: [-1 1]
  

The NumFactors field of the VolSpec structure, VolsSpec.NumFactors = 1, reveals that the number of factors used to generate VolSpec was one. The FactorModels field indicates that it is a 'Constant' factor, and the NumBranches field indicates the number of branches. As a consequence, each node of the resulting tree has two branches, one going up, and the other going down.

Consider now a two-factor volatility process made from a proportional factor and an exponential factor.

• % Exponential factor:
  Sigma_0 = 0.1;
  Lambda = 1;
  % Proportional factor
  CurveProp = [0.11765; 0.08825; 0.06865];
  CurveTerm = [   1   ;    2   ;    3   ];
  % Build VolSpec
  VolSpec = hjmvolspec('Proportional', CurveProp, CurveTerm,... 
  1e6,'Exponential', Sigma_0, Lambda)
  
  VolSpec = 
  
        FinObj: 'HJMVolSpec'
  FactorModels: {'Proportional'  'Exponential'}
    FactorArgs: {{1x3 cell}  {1x2 cell}}
    SigmaShift: 0
    NumFactors: 2
     NumBranch: 3
       PBranch: [0.2500 0.2500 0.5000]
   Fact2Branch: [2x3 double]
  

The output shows that the volatility specification was generated using two factors. The tree has three branches per node. Each branch has probabilities of 0.25, 0.25, and 0.5, going from top to bottom.

Specifying the Interest Rate Term Structure (RateSpec)

The structure RateSpec is an interest term structure that defines the initial forward rate specification from which the tree rates are derived. The section Interest Rate Term Structure explains how to create these structures using the function intenvset, given the interest rates, the starting and ending dates for each rate, and the compounding value.

Consider the example

• Compounding = 1;
  Rates = [0.02; 0.02; 0.02; 0.02];
  StartDates = ['01-Jan-2000';   
                '01-Jan-2001';  
                '01-Jan-2002';  
                '01-Jan-2003'];
  EndDates =   ['01-Jan-2001'; 
                '01-Jan-2002';  
                '01-Jan-2003'; 
                '01-Jan-2004'];
  ValuationDate = '01-Jan-2000';
  
  RateSpec = intenvset('Compounding',1,'Rates', Rates,... 
  'StartDates', StartDates, 'EndDates', EndDates,...
  'ValuationDate', ValuationDate)
  
  RateSpec = 
  
          FinObj: 'RateSpec'
     Compounding: 1
            Disc: [4x1 double]
           Rates: [4x1 double]
        EndTimes: [4x1 double]
      StartTimes: [4x1 double]
        EndDates: [4x1 double]
      StartDates: [4x1 double]
   ValuationDate: 730486
           Basis: 0
    EndMonthRule: 1
  

Use the function datedisp to examine the dates defined in the variable RateSpec. For example

• datedisp(RateSpec.ValuationDate)
  01-Jan-2000
  

Specifying the Time Structure (TimeSpec)

The structure TimeSpec specifies the time structure for an HJM tree. This structure defines the mapping between the observation times at each level of the tree and the corresponding dates.

TimeSpec is built using the function hjmtimespec. The hjmtimespec function requires three input arguments:

• The valuation date ValuationDate
• The maturity date Maturity
• The compounding rate Compounding

The syntax used for calling hjmtimespec is

• TimeSpec = hjmtimespec(ValuationDate, Maturity, Compounding)
  

where:

• ValuationDate is the first observation date in the tree.
• Maturity is a vector of dates representing the cash flow dates of the tree. Any instrument cash flows with these maturities fall on tree nodes.
• Compounding is the frequency at which the rates are compounded when annualized.

Calling hjmtimespec with the same data used to create the interest rate term structure, RateSpec builds the structure that specifies the time layout for the tree.

• Maturity = EndDates;
  TimeSpec = hjmtimespec(ValuationDate, Maturity, Compounding)
  
  TimeSpec = 
  
         FinObj: 'HJMTimeSpec'
  ValuationDate: 730486
       Maturity: [4x1 double]
    Compounding: 1
          Basis: 0
   EndMonthRule: 1
  

Note that the maturities specified when building TimeSpec do not have to coincide with the EndDates of the rate intervals in RateSpec. Since TimeSpec defines the time-date mapping of the HJM tree, the rates in RateSpec are interpolated to obtain the initial rates with maturities equal to those found in TimeSpec.

Example: Creating an HJM Tree

Use the VolSpec, RateSpec, and TimeSpec you have created as input to the HJMTree function to create an HJM tree.

• % Reset the volatility factor to the Constant case
  VolSpec = hjmvolspec('Constant', 0.10);
  
  HJMTree = hjmtree(VolSpec, RateSpec, TimeSpec)
  
  HJMTree = 
  
    FinObj: 'HJMFwdTree'
   VolSpec: [1x1 struct]
  TimeSpec: [1x1 struct]
  RateSpec: [1x1 struct]
      tObs: [0 1 2 3]
      TFwd: {[4x1 double] [3x1 double] [2x1 double] [3]}
    CFlowT: {[4x1 double] [3x1 double] [2x1 double] [4]}
   FwdTree:{[4x1 double][3x1x2 double][2x2x2 double][1x4x2 double]}
  

Sensitivity

Using HJM Trees in MATLAB