Least Squares Polynomial Fit (DSP Blockset)

Compute the coefficients of the polynomial that best fits the input data in a least-squares sense.

Library

Description

The Least Squares Polynomial Fit block computes the coefficients of the nth order polynomial that best fits the input data in the least-squares sense, where n is specified by the Polynomial order parameter. A distinct set of n+1 coefficients is computed for each column of the M-by-N input, u.

For a given input column, the block computes the set of coefficients, c₁, c₂, ..., c_n₊₁, that minimizes the quantity

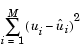
where u_i is the ith element in the input column, and

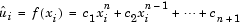
The values of the independent variable, x₁, x₂, ..., x_M, are specified as a length-M vector by the Control points parameter. The same M control points are used for all N polynomial fits, and can be equally or unequally spaced. The equivalent MATLAB code is shown below.

c = polyfit(x,u,n)       % Equivalent MATLAB code

Inputs can be frame-based or sample-based. For convenience, a length-M 1-D vector input is treated as an M-by-1 matrix.

Each column of the (n+1)-by-N output matrix, c, represents a set of n+1 coefficients describing the best-fit polynomial for the corresponding column of the input. The coefficients in each column are arranged in order of descending exponents, c₁, c₂, ..., c_n₊₁. The output is always sample-based.

Example

In the model below, the Polynomial Evaluation block uses the second-order polynomial

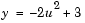
to generate four values of dependent variable y from four values of independent variable u, received at the top port. The polynomial coefficients are supplied in the vector [-2 0 3] at the bottom port. Note that the coefficient of the first-order term is zero.

The Control points parameter of the Least Squares Polynomial Fit block is configured with the same four values of independent variable u that are used as input to the Polynomial Evaluation block, [1 2 3 4]. The Least Squares Polynomial Fit block uses these values together with the input values of dependent variable y to reconstruct the original polynomial coefficients.

Dialog Box

Control points: The values of the independent variable to which the data in each input column correspond. For an M-by-N input, this parameter must be a length-M vector. Tunable.
Polynomial order: The order, n, of the polynomial to be used in constructing the best fit. The number of coefficients is n+1. Tunable.

Supported Data Types

Double-precision floating point
Single-precision floating point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

Detrend
DSP Blockset

Polynomial Evaluation
DSP Blockset

Polynomial Stability Test
DSP Blockset

polyfit
MATLAB

Detrend	DSP Blockset
Polynomial Evaluation	DSP Blockset
Polynomial Stability Test	DSP Blockset
`polyfit`	MATLAB

Also see Polynomial Functions for a list of all the blocks in the Polynomial Functions library.

LDL Solver Levinson-Durbin