

| DSP Blockset |   |
Determine whether all roots of the input polynomial are inside the unit circle using the Schur-Cohn algorithm.
Library
Math Functions / Polynomial Functions
Description
The Polynomial Stability Test block uses the Schur-Cohn algorithm to determine whether all roots of a polynomial are within the unit circle.
Each column of the M-by-N input matrix u contains M coefficients from a distinct polynomial,
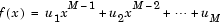
arranged in order of descending exponents, u1, u2, ..., uM. The polynomial has order M-1 and positive integer exponents.
Inputs can be frame-based or sample-based, and both represent the polynomial coefficients as shown above. For convenience, a length-M 1-D vector input is treated as an M-by-1 matrix.
The output is a 1-by-N matrix with each column containing the value 1 or 0. The value 1 indicates that the polynomial in the corresponding column of the input is stable; i.e., the magnitudes of all solutions to f(x) = 0 are less than 1. The value 0 indicates that the polynomial in the corresponding column of the input may be unstable; i.e., the magnitude of at least one solution to f(x) = 0 is greater than or equal to 1.
The output is always sample-based.
Applications
This block is most commonly used to check the pole locations of the denominator polynomial, A(z), of a transfer function, H(z).
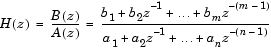
The poles are the n-1 roots of the denominator polynomial, A(z). If any poles are located outside the unit circle, the transfer function H(z) is unstable. As is typical in DSP applications, the transfer function above is specified in descending powers of z-1 rather than z.
Dialog Box
Supported Data Types
To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.
See Also
| Least Squares Polynomial Fit |
DSP Blockset |
| Polynomial Evaluation |
DSP Blockset |
polyfit |
MATLAB |
Also see Polynomial Functions for a list of all the blocks in the Polynomial Functions library.
 | Polynomial Evaluation | Pseudoinverse |  |