Interpolation (DSP Blockset)

Interpolate values of real input samples

Library

Description

The Interpolation block interpolates each channel of discrete, real, inputs using linear or FIR interpolation. The input can be a sample- or frame-based vector or matrix. The output is a vector or matrix of the interpolated values, and has the same frame status and frame rate as the input.

You must specify the interpolation points (times at which to interpolate values) in an interpolation vector, I_n. An entry of 1 in I_n refers to the first sample of the input, an entry of 2.5 refers to the sample half-way between the second and third input sample, and so on. I_n must have the same frame status and frame rate as the input, and can be a length-P row or column vector, where P is usually any positive integer.

Usually, the block applies the vector I_n to each column of an input matrix, or to each input vector. You can set the block to either apply the same interpolation vector for all input vectors or matrices (static interpolation points), or use a different interpolation vector for each input vector or matrix (time-varying interpolation points).

For more information, see other sections of this reference page.

Sections of This Reference Page

Specifying Static Interpolation Points

To supply the block with a static interpolation vector (an interpolation vector applied to every input vector or matrix), do the following:

Set the Source of interpolation points parameter to Parameter.
Enter the interpolation vector in the Interpolation points parameter. To learn about interpolation vectors, see How the Block Applies Interpolation Vectors to Inputs.

Specifying Time-Varying Interpolation Points

To supply the block with time-varying interpolation vectors (where the block uses a different interpolation vector for each input vector or matrix), do the following:

Set the Source of interpolation points parameter to Input port, which activates a block input port, In, for the interpolation points.
Generate a signal of interpolation vectors with the same frame status and same frame rate as the input signal, and supply it to the input port for interpolation points. To learn about interpolation vectors, see How the Block Applies Interpolation Vectors to Inputs.

How the Block Applies Interpolation Vectors to Inputs

The interpolation vector I_n represents the points in time at which to interpolate values of the input signal. An entry of 1 in I_n refers to the first sample of the input, an entry of 2.5 refers to the sample half-way between the second and third input sample, and so on. In most cases, the vector I_n can be of any length.

Depending on the dimension and frame status of the input and the dimension of I_n, the block usually applies I_nto the input in one of the following ways:

Apply the vector I_n to each channel of a matrix input, resulting in a matrix output.
Apply the vector I_n to each input vector (as if the input vector were a single channel), resulting in a vector output with the same orientation as the input (row or column).

The following tables summarize how the block applies the vector I_n to all the possible types of sample- and frame-based inputs, and show the resulting output dimensions. (The block applies both static and time-varying interpolation vectors to the input signal in the same way).

Table 7-12: How Block Applies Interpolation Vectors to Frame-Based Inputs
Frame-Based Input Dimensions
Dimensions of Interpolation Vector I_n
P is a positive integer
How Block Applies I_n to Input
Frame-Based Output Dimensions

M-by-N matrix
P-by-1 column
Applies I_n to each input column
P-by-N matrix

1-by-N row
Applies each column of I_n (each element of I_n) to the corresponding columns of the input
1-by-N row

M-by-1 column
P-by-1 column
Applies I_n to the input column
P-by-1 column

1-by-P row
(block treats as a column)
Applies I_n to the input column
P-by-1 column

1-by-N row
(not recommended)
P-by-1 column
not applicable
P-by-N matrix where each row is a copy of the input vector

1-by-P row
not applicable
1-by-N row, a copy of the input vector

**Table 7-12: How Block Applies Interpolation Vectors to Frame-Based Inputs**
Frame-Based Input Dimensions	Dimensions of Interpolation Vector I_n P is a positive integer	How Block Applies I_n to Input	Frame-Based Output Dimensions
M-by-N matrix	P-by-1 column	Applies I_n to each input column	P-by-N matrix
1-by-N row	Applies each column of I_n (each element of I_n) to the corresponding columns of the input	1-by-N row
M-by-1 column	P-by-1 column	Applies I_n to the input column	P-by-1 column
1-by-P row (block treats as a column)	Applies I_n to the input column	P-by-1 column
1-by-N row (not recommended)	P-by-1 column	not applicable	P-by-N matrix where each row is a copy of the input vector
1-by-P row	not applicable	1-by-N row, a copy of the input vector

Table 7-13: How Block Applies Interpolation Vectors to Sample-Based Inputs
Sample-Based Input Dimensions
Dimensions of Interpolation Vector I_n
P is any positive integer
How Block Applies I_n to Input
Sample-Based Output Dimensions

M-by-N matrix
P-by-1 column
Applies I_n to each input column
P-by-N matrix

1-by-P row
(block treats as a column)
Applies I_n to each input column
P-by-N matrix

M-by-1 column
P-by-1 column
Applies I_n to the input column
P-by-1 column

1-by-P row
(block treats as a column)
Applies I_n to the input column
P-by-1 column

1-by-N row
P-by-1 column
(block treats as a row)
Applies I_n to the input row
1-by-P row

1-by-P row
Applies I_n to the input row
1-by-P row

**Table 7-13: How Block Applies Interpolation Vectors to Sample-Based Inputs**
Sample-Based Input Dimensions	Dimensions of Interpolation Vector I_n P is any positive integer	How Block Applies I_n to Input	Sample-Based Output Dimensions
M-by-N matrix	P-by-1 column	Applies I_n to each input column	P-by-N matrix
1-by-P row (block treats as a column)	Applies I_n to each input column	P-by-N matrix
M-by-1 column	P-by-1 column	Applies I_n to the input column	P-by-1 column
1-by-P row (block treats as a column)	Applies I_n to the input column	P-by-1 column
1-by-N row	P-by-1 column (block treats as a row)	Applies I_n to the input row	1-by-P row
1-by-P row	Applies I_n to the input row	1-by-P row

Handling Out-of-Range Interpolation Points

The valid range of the values in the interpolation vector I_n is from 1 to the number of samples in each channel of the input. For instance, given a length-5 input vector D, all entries of I_n must range from 1 to 5. I_n cannot contain entries such as 7 or -9, since there is no 7th or -9th entry in D.

The Out of range interpolation points parameter sets how the block handles interpolation points that are not within the valid range, and has the following settings:

Clip -- The block replaces any out-of-range values in I_n with the closest value in the valid range (from 1 to the number of input samples), and then proceeds with computations using the clipped version of I_n.
Clip and warn -- In addition to Clip, the block issues a warning at the MATLAB command line every time clipping occurs.
Error -- When the block encounters an out-of-range value in I_n, the simulation stops and the block issues an error at the MATLAB command line.

Example of Clipping . Suppose the block is set to clip out-of-range interpolation points, and gets the following input vector and interpolation points:

D = [11, 22, 33, 44]'
I_n = [10, 2.6, -3]'

Since D has 4 samples, valid interpolation points range from 1 to 4. The block clips the interpolation point 10 to 4 and the point -3 to 1, resulting in the clipped interpolation vector I_nclipped = [4, 2.6, 1]'.

Linear Interpolation Mode

When Interpolation Mode is set to Linear, the block interpolates data values by assuming that the data varies linearly between samples taken at adjacent sample times.

For instance, if the input signal D = [1, 2, 1.5, 3, 0.25]', the following left-hand plot shows the samples in D, and the right-hand plot shows the linearly interpolated values between the samples in D.

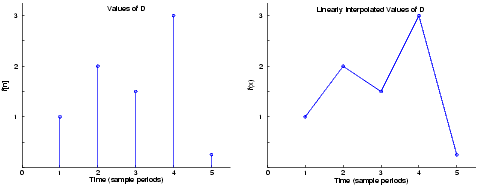
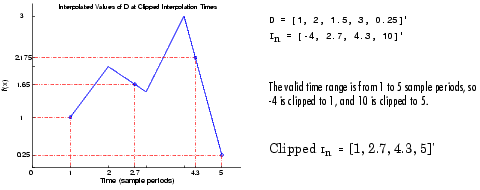
As illustrated below, if the block is in linear interpolation mode and is set to clip out-of-range interpolation points, where

D = [1, 2, 1.5, 3, 0.25]'
I_n = [-4, 2.7, 4.3, 10]'

then the block clips the invalid interpolation points, and outputs the linearly interpolated values in a vector, [1, 1.65, 2.175, 0.25]'.

FIR Interpolation Mode

When Interpolation Mode is set to FIR, the block interpolates data values using an FIR interpolation filter, specified by various block parameters. See the topic on FIR Interpolation Mode in the Variable Fractional Delay block reference for more information.

Dialog Box

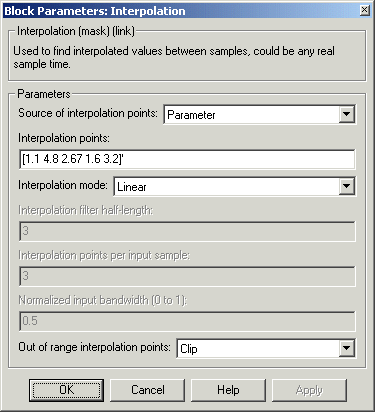
Source of interpolation points: Sets the location for specifying interpolation points (the points in time at which to interpolate the input): either in a dialog parameter (for static interpolation points) or a block input port (for time-varying interpolation points). For more information, see Specifying Static Interpolation Points and Specifying Time-Varying Interpolation Points. Tunable.
Interpolation points: The vector I_nof points in time at which to interpolate the input signal. An entry of 1 in I_n refers to the first sample of the input, an entry of 2.5 refers to the sample half-way between the second and third input sample, and so on. See How the Block Applies Interpolation Vectors to Inputs. Tunable.
Interpolation mode: Sets the block to interpolate by either linear or FIR interpolation. For more information, see Linear Interpolation Mode and FIR Interpolation Mode.
Interpolator filter half-length: Half the length of the FIR interpolation filter. For more information, see FIR Interpolation Mode.
Interpolation points per input sample: The number Q, where the FIR interpolation filter uses the nearest 2*Q points in the signal to interpolate the value at an interpolation point. If there are less than 2*Q neighboring points, the block uses linear interpolation in place of FIR interpolation. For more information, see FIR Interpolation Mode. and Linear Interpolation Mode.
Normalized input bandwidth (0 to 1): The bandwidth of the input divided by Fs/2 (half the input sample frequency). For more information, see FIR Interpolation Mode.
Out of range interpolation points: If an interpolation point is out of range, this parameter sets the block to either clip the interpolation point, clip the value and issue a warning at the MATLAB command line, or stop the simulation and issue an error at the MATLAB command line. For more information, see Handling Out-of-Range Interpolation Points.

Supported Data Types

Double-precision floating point
Single-precision floating point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

See Signal Operations for a list of all the blocks in the Signal Operations library.

Integer Delay Kalman Adaptive Filter