Variable Fractional Delay (DSP Blockset)

Delay an input by a time-varying fractional number of sample periods.

Library

Description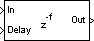

The Variable Fractional Delay block delays each channel of the M_i-by-N input matrix, u, by a variable (possibly noninteger) number of sample intervals.

The block computes the value for each channel of the output based on the stored samples in memory most closely indexed by the Delay input, v, and the interpolation method specified by the Mode parameter. In Linear Interpolation mode, the block stores the D+1 most recent samples received at the In port for each channel, where D is the Maximum delay. In FIR Interpolation mode, the block stores the D+P+1 most recent samples received at the In port for each channel, where P is the Interpolation filter half-length.

See the Variable Integer Delay block for further discussion of how input samples are stored in the block's memory. The Variable Fractional Delay block differs only in the way that these stored sample are accessed; a fractional delay requires the computation of a value by interpolation from the nearby samples in memory.

Sample-Based Operation

When the input is sample-based, the block treats each of the M_i*N matrix elements as an independent channel. The input to the Delay port, v, is an M_i-by-N matrix of floating-point values in the range 0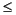 v 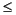D that specifies the number of sample intervals to delay each channel of the input.

A 1-D vector input is treated as an M_i-by-1 matrix, and the output is 1-D.

The Initial conditions parameter specifies the values in the block's memory at the start of the simulation in the same manner as for the Variable Integer Delay block. See the section on sample-based initial conditions there for complete information.

Frame-Based Operation

When the input is frame-based, the block treats each of the N input columns as a frame containing M_i sequential time samples from an independent channel.

The input to the Delay port, v, contains floating-point values in the range 0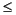 v 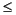D specifying the number of sample intervals to delay the current input. The input to the Delay port can be:

An M_i-by-N matrix containing the number of sample intervals to delay each sample in each channel of the current input
An M_i-by-1 matrix containing the number of sample intervals to delay each sample in every channel of the current input
A 1-by-N matrix containing the number of sample intervals to delay every sample in each channel of the current input

For example, if v is the M_i-by-1 matrix [v(1) v(2) ... v(Mi)]', the earliest sample in the current frame is delayed by v(1) fractional sample intervals, the following sample in the frame is delayed by v(2) fractional sample intervals, and so on. The set of fractional delays contained in v is applied identically to every channel of a multichannel input.

The Initial conditions parameter specifies the values in the block's memory at the start of the simulation in the same manner as for the Variable Integer Delay block. See the section on frame-based initial conditions there for complete information.

Interpolation Modes

The delay value specified at the Delay port is used as an index into the block's memory, U, which stores the D+1 most recent samples received at the In port for each channel. For example, an integer delay of 5 on a scalar input sequence retrieves and outputs the fifth most recent input sample from the block's memory, U(6). Fractional delays are computed by interpolating between stored samples; the two available interpolation modes are described below.

Linear Interpolation Mode. For noninteger delays, at each sample time the Linear Interpolation mode uses the two samples in memory nearest to the specified delay to compute a value for the sample at that time. If v is the specified fractional delay for a scalar input, the output sample, y, is computed as follows.

vi = floor(v)                     % vi = integer delay
vf = v-vi                         % vf = fractional delay
y = (1-vf)*U(vi) + vf*U(vi+1)

Delay values less than 0 are clipped to 0, and delay values greater than D are clipped to D, where D is the Maximum delay. Note that a delay value of 0 causes the block to pass through the current input sample, U(1), in the same simulation step that it is received.

FIR Interpolation Mode. In FIR Interpolation mode, the block computes a value for the sample at the desired delay by applying an FIR filter of order 2P to the stored samples on either side of the desired delay, where P is the Interpolation filter half-length. For periodic signals, a larger value of P (i.e., a higher order filter) yields a better estimate of the sample at the specified delay. A value between 4 and 6 for this parameter (i.e. a 7th to 11th order filter) is usually adequate.

A vector of 2P filter tap weights is precomputed at the start of the simulation for each of Q-1 discrete points between input samples, where Q is specified by the Interpolation points per input sample parameter. For a delay corresponding to one of the Q interpolation points, the unique filter computed for that interpolation point is applied to obtain a value for the sample at the specified delay. For delay times that fall between interpolation points, the value computed at the nearest interpolation point is used. Since Q controls the number of locations where a unique interpolation filter is designed, a larger value results in a better estimate of the sample at a given delay.

Note that increasing the Interpolation filter half length (P) increases the number of computations performed per input sample, as well as the amount of memory needed to store the filter coefficients. Increasing the Interpolation points per input sample (Q) increases the simulation's memory requirements but does not affect the computational load per sample.

The Normalized input bandwidth parameter allows you to take advantage of the bandlimited frequency content of the input. For example, if you know that the input signal does not have frequency content above F_s/4, you can specify a value of 0.5 for the Normalized input bandwidth to constrain the frequency content of the output to that range.

(Each of the Q interpolation filters can be considered to correspond to one output phase of an "upsample-by-Q" FIR filter. In this view, the Normalized input bandwidth value is used to improve the stopband in critical regions, and to relax the stopband requirements in frequency regions where there is no signal energy.)

For delay values less than P/2-1, the output is computed using linear interpolation. Delay values greater than D are clipped to D, where D is the Maximum delay.

The block uses the intfilt function in the Signal Processing Toolbox to compute the FIR filters.

Note When the Variable Fractional Delay block is used in a feedback loop, at least one block with nonzero delay (e.g., an Integer Delay block with Delay > 0) should be included in the loop as well. This prevents the occurrence of an algebraic loop if the delay of the Variable Fractional Delay block is driven to zero.

Examples

The dspafxf demo illustrates an audio flanger system built around the Variable Fractional Delay block.

Dialog Box

Mode: The method by which to interpolate between adjacent stored samples to obtain a value for the sample indexed by the input at the Delay port.
Maximum delay: The maximum delay that the block can produce, D. Delay input values exceeding this maximum are clipped at the maximum.
Interpolation filter half-length: Half the number of input samples to use in the FIR interpolation filter.
Interpolation points per input sample: The number of points per input sample, Q, at which a unique FIR interpolation filter is computed.
Normalized input bandwidth: The bandwidth to which the interpolated output samples should be constrained. A value of 1 specifies half the sample frequency.
Initial conditions: The values with which the block's memory is initialized. See the Variable Integer Delay block for more information.

Supported Data Types

Double-precision floating point
Single-precision floating point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

Integer Delay
DSP Blockset

Unit Delay
Simulink

Variable Integer Delay
DSP Blockset

Integer Delay	DSP Blockset
Unit Delay	Simulink
Variable Integer Delay	DSP Blockset

Also see Signal Operations for a list of all the blocks in the Signal Operations library.

Upsample Variable Integer Delay