

| DSP Blockset |   |
Compute an estimate of AR model parameters using the covariance method.
Library
Estimation / Parametric Estimation
Description
The Covariance AR Estimator block uses the covariance method to fit an autoregressive (AR) model to the input data. This method minimizes the forward prediction error in the least-squares sense.
The input is a sample-based vector (row, column, or 1-D) or frame-based vector (column only) representing a frame of consecutive time samples from a single-channel signal, which is assumed to be the output of an AR system driven by white noise. The block computes the normalized estimate of the AR system parameters, A(z), independently for each successive input frame.
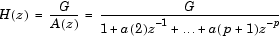
The order, p, of the all-pole model is specified by the Estimation order parameter. To guarantee a nonsingular output, you must set the value of p to be less than the input length. Otherwise, the output may be singular.
The top output, A, is a column vector of length p+1 with the same frame status as the input, and contains the normalized estimate of the AR model coefficients in descending powers of z,
The scalar gain, G, is provided at the bottom output (G).
Dialog Box
References
Kay, S. M. Modern Spectral Estimation: Theory and Application. Englewood Cliffs, NJ: Prentice-Hall, 1988.
Marple, S. L., Jr., Digital Spectral Analysis with Applications. Englewood Cliffs, NJ: Prentice-Hall, 1987.
Supported Data Types
To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.
See Also
| Burg AR Estimator |
DSP Blockset |
| Covariance Method |
DSP Blockset |
| Modified Covariance AR Estimator |
DSP Blockset |
| Yule-Walker AR Estimator |
DSP Blockset |
arcov |
Signal Processing Toolbox |
Also see Parametric Estimation for a list of all the blocks in the Parametric Estimation library.
 | Counter | Covariance Method |  |