Curve Fitting Toolbox

Basic Assumptions About the Error

When fitting data that contains random variations, there are two important assumptions that are usually made about the error:

• The error exists only in the response data, and not in the predictor data.
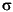• The errors are random and follow a normal (Gaussian) distribution with zero mean and constant variance, ².

The second assumption is often expressed as

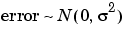
The components of this expression are described below.

Normal Distribution

The errors are assumed to be normally distributed because the normal distribution often provides an adequate approximation to the distribution of many measured quantities. Although the least squares fitting method does not assume normally distributed errors when calculating parameter estimates, the method works best for data that does not contain a large number of random errors with extreme values. The normal distribution is one of the probability distributions in which extreme random errors are uncommon. However, statistical results such as confidence and prediction bounds do require normally distributed errors for their validity.

Zero Mean

If the mean of the errors is zero, then the errors are purely random. If the mean is not zero, then it might be that the model is not the right choice for your data, or the errors are not purely random and contain systematic errors.

Constant Variance

A constant variance in the data implies that the "spread" of errors is constant. Data that has the same variance is sometimes said to be of equal quality.

The assumption that the random errors have constant variance is not implicit to weighted least squares regression. Instead, it is assumed that the weights provided in the fitting procedure correctly indicate the differing levels of quality present in the data. The weights are then used to adjust the amount of influence each data point has on the estimates of the fitted coefficients to an appropriate level.

Parametric Fitting

The Least Squares Fitting Method