Integer-Input RS Encoder (Communications Blockset)

Create a Reed-Solomon code from integer vector data

Library

Block sublibrary of Channel Coding

Description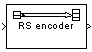

The Integer-Input RS Encoder block creates a Reed-Solomon code with message length K and codeword length N. You specify both N and K directly in the block mask. The symbols for the code are integers between 0 and 2^M-1, which represent elements of the finite field GF(2^M). Restrictions on M and N are described in the section Restrictions on M and the Codeword Length N below. The difference N - K must be an even integer.

The input and output are integer-valued signals that represent messages and codewords, respectively. The input must be a frame-based column vector whose length is an integer multiple of K. The output is a frame-based column vector whose length is the same integer multiple of N. For more information on representing data for Reed-Solomon codes, see the section Integer Format (Reed-Solomon only)."

The default value of M is the smallest integer that is greater than or equal to log2(N+1), that is, ceil(log2(N+1)). You can change the value of M from the default by specifying the primitive polynomial for GF(2^M), as described in the section Specifying the Primitive Polynomial following. If N is less than 2^M-1, the block uses a shortened Reed-Solomon code.

An (N, K) Reed-Solomon code can correct up to floor((N-K)/2) symbol errors (not bit errors) in each codeword.

Specifying the Primitive Polynomial

You can specify the primitive polynomial that defines the finite field GF(2^M), corresponding to the integers that form messages and codewords. To do so, first check the box next to Specify primitive polynomial. Then, in the Primitive polynomial field, enter a binary row vector that represents a primitive polynomial over GF(2) of degree M, in descending order of powers. For example, to specify the polynomial 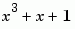, enter the vector [1 0 1 1].

If you do not select the box next to Specify primitive polynomial, the block uses the default primitive polynomial of degree M = ceil(log2(N+1)). You can display the default polynomial by entering primpoly(ceil(log2(N+1))) at the MATLAB prompt.

Restrictions on M and the Codeword Length N

The restrictions on the degree M of the primitive polynomial and the codeword length N are as follows:

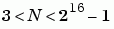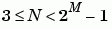If you do not select the box next to Specify primitive polynomial, N must lie in the range .
If you do select the box next to Specify primitive polynomial, N must lie in the range and M must lie in the range .

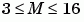Specifying the Generator Polynomial

You can specify the generator polynomial for the Reed-Solomon code. To do so, first select the box next to Specify generator polynomial. Then, in the Generator polynomial field, enter an integer row vector whose entries are between 0 and 2^M-1. The vector represents a polynomial, in descending order of powers, whose coefficients are elements of GF(2^M) represented in integer format. See the section Integer Format (Reed-Solomon only) for more information about integer format. The generator polynomial must be equal to a polynomial with a factored form

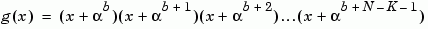
where 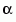is the primitive element of the Galois field over which the input message is defined, and b is an integer.

If you do not select the box next to Specify generator polynomial, the block uses the default generator polynomial, corresponding to b=1, for Reed-Solomon encoding. You can display the default generator polynomial by typing rsgenpoly(N1,K1), where N1 = 2M-1 and K1 = K+(N1-N), at the MATLAB prompt, if you are using the default primitive polynomial. If the Specify primitive polynomial box is selected, and you specify the primitive polynomial specified as poly, the default generator polynomial is rsgenpoly(N1,K1,poly).

Examples

Suppose M = 3, N = 2³-1 = 7, and K = 5. Then a message is a vector of length 5 whose entries are integers between 0 and 7. A corresponding codeword is a vector of length 7 whose entries are integers between 0 and 7. The following figure illustrates possible input and output signals to this block when Codeword length N is set to 7, Message length K is set to 5, and the default primitive and generator polynomials are used.

Dialog Box

Codeword length N: The codeword length.
Message length K: The message length.
Specify primitive polynomial: When you select this box, you can specify the primitive polynomial as a binary row vector.
Primitive polynomial: Binary row vector representing the primitive polynomial in descending order of powers.
Specify generator polynomial: When you select this box, you can specify the generator polynomial as an integer row vector.
Generator polynomial: Integer row vector, whose entries are in the range from 0 to 2^M-1, representing the generator polynomial in descending order of powers.

Pair Block

Integer-Output RS Decoder

See Also

Binary-Input RS Encoder

Insert Zero Integer-Output RS Decoder