Binary-Input RS Encoder (Communications Blockset)

Create a Reed-Solomon code from binary vector data

Library

Block sublibrary of Channel Coding

Description

The Binary-Input RS Encoder block creates a Reed-Solomon code with message length K and codeword length N. You specify both N and K directly in the block mask. The symbols for the code are binary sequences of length M, corresponding to elements of the Galois field GF(2^M), where the first bit in each sequence is the most significant bit. Restrictions on M and N are given in the section Restrictions on the M and the Codeword Length N below. The difference N-K must be an even integer.

The input and output are binary-valued signals that represent messages and codewords, respectively. The input must be a frame-based column vector whose length is an integer multiple of M*K. The output is a frame-based column vector whose length is the same integer multiple of M*N. For more information on representing data for Reed-Solomon codes, see the section Integer Format (Reed-Solomon only)."

The default value of M is the smallest integer that is greater than or equal to log2(N+1), that is, ceil(log2(N+1)). You can change the value of M from the default by specifying the primitive polynomial for GF(2^M), as described in the section Specifying the Primitive Polynomial following. If N is less than 2^M-1, the block uses a shortened Reed-Solomon code.

Each M*K input bits represent K integers between 0 and 2^M-1. Similarly, each M*N output bits represent N integers between 0 and 2^M-1. These integers in turn represent elements of the Galois field GF(2^M).

An (N,K) Reed-Solomon code can correct up to floor((N-K)/2) symbol errors (not bit errors) in each codeword.

Specifying the Primitive Polynomial

You can specify the primitive polynomial that defines the finite field GF(2^M), corresponding to the integers that form messages and codewords. To do so, first select the box next to Specify primitive polynomial. Then, in the Primitive polynomial field, enter a binary row vector that represents a primitive polynomial over GF(2) of degree M, in descending order of powers. For example, to specify the polynomial 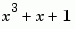, enter the vector [1 0 1 1].

If you do not select the box next to Specify primitive polynomial, the block uses the default primitive polynomial of degree M = ceil(log2(N+1)). You can display the default polynomial by entering primpoly(ceil(log2(N+1))) at the MATLAB prompt.

Restrictions on the M and the Codeword Length N

The restrictions on the degree M of the primitive polynomial and the codeword length N are as follows:

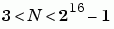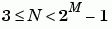If you do not select the box next to Specify primitive polynomial, N must lie in the range .
If you do select the box next to Specify primitive polynomial, N must lie in the range and M must lie in the range .

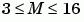Specifying the Generator Polynomial

You can specify the generator polynomial for the Reed-Solomon code. To do so, first select the box next to Specify generator polynomial. Then, in the Generator polynomial field, enter an integer row vector whose entries are between 0 and 2^M-1. The vector represents a polynomial, in descending order of powers, whose coefficients are elements of GF(2^M) represented in integer format. See the section Integer Format (Reed-Solomon only) for more information about integer format. The generator polynomial must be equal to a polynomial with a factored form

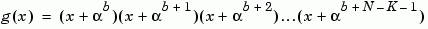
where 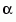is the primitive element of the Galois field over which the input message is defined, and b is a non-negative integer.

If you do not select the box next to Specify generator polynomial, the block uses the default generator polynomial, corresponding to b=1, for Reed-Solomon encoding. You can display the default generator polynomial by typing rsgenpoly(N1,K1), where N1=2M-1 and K1=K+(N1-N), at the MATLAB prompt, if you are using the default primitive polynomial. If the Specify primitive polynomial box is selected, and you specify the primitive polynomial specified as poly, the default generator polynomial is rsgenpoly(N1,K1,poly).

Examples

Suppose M = 3, N = 2³-1 = 7, and K = 5. Then a message is a binary vector of length 15 that represents 5 three-bit integers. A corresponding codeword is a binary vector of length 21 that represents 7 three-bit integers. The following figure shows the codeword that would result from a particular message word. The integer format equivalents illustrate that the highest order bit is at the left.

Dialog Box

Codeword length N: The codeword length. The output has vector length M*N.
Message length K: The message length. The input has vector length M*K.
Specify primitive polynomial: When you select this box, you can specify the primitive polynomial as a binary row vector.
Primitive polynomial: Binary row vector representing the primitive polynomial in descending order of powers.
Specify generator polynomial: When you select this box, you can specify the generator polynomial as an integer row vector.
Generator polynomial: Integer row vector, whose entries are in the range from 0 to 2^M-1, representing the generator polynomial in descending order of powers.

Pair Block

Binary-Output RS Decoder

See Also

Integer-Input RS Encoder

Binary Error Pattern Generator Binary Linear Decoder