Aerospace Blockset

Wind Shear Model

Calculate wind shear conditions

Library

Environment/Wind

Description

The Wind Shear Model block adds wind shear to the aerospace model. This implementation is based on the mathematical representation in the Military Specification MIL-F-8785C [1]. The magnitude of the wind shear is given by the following equation for the mean wind profile as a function of altitude and the measured wind speed at 20 feet (6 m) above the ground.

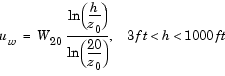
where u_w is the mean wind speed, W₂₀ is the measured wind speed at an altitude of 20 feet, 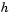is the altitude, and 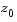is a constant equal to 0.15 feet for Category C flight phases and 2.0 feet for all other flight phases. Category C flight phases are defined in reference [1] to be terminal flight phases, which include takeoff, approach, and landing.

The resultant mean wind speed in the Earth-fixed axis frame is changed to body-fixed axis coordinates by multiplying by the direction cosine matrix (DCM) input to the block. The block output is the mean wind speed in the body-fixed axis.

Dialog Box

Flight Phase

Select flight phase:

• Category C - Terminal Flight Phases
• Other

Wind speed at 20 feet (or 6 m) altitude (meters/second, feet/second, or knots)

The measured wind speed at an altitude of 20 feet (6 m) above the ground.

Wind direction at 20 feet altitude (degrees clockwise from north)

The direction of the wind at an altitude of 20 feet (6 m), measured in degrees clockwise from the direction of the Earth x-axis (north). The wind direction is defined as the direction from which the wind is coming.

Inputs and Outputs

The first input is altitude, in units selected.

The second input is a 3-by-3 direction cosine matrix.

The output is a 3-by-1 vector of the mean wind speed in the body axes frame, in the selected units.

Examples

See the aeroblk_HL20.mdl example included with the blockset.

References

Military Specification MIL-F-8785C, 5th November, 1980.

See Also
Discrete Wind Gust Model

Dryden Wind Turbulence Model

WGS84 Gravity Model