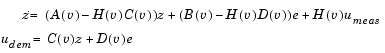2D Self-Conditioned [A(v),B(v),C(v),D(v)] (Aerospace Blockset)

2D Self-Conditioned [A(v),B(v),C(v),D(v)]

Implement a gain-scheduled state-space controller in a self-conditioned form

Library

GNC

Description

The 2D Self-Conditioned [A(v),B(v),C(v),D(v)] block implements a gain-scheduled state-space controller as defined by the equations

in the self-conditioned form

For the rationale behind this self-conditioned implementation, refer to the Self-Conditioned [A,B,C,D] block reference. This block implements a gain-scheduled version of the Self-Conditioned [A,B,C,D] block, v being the vector of parameters over which A, B, C, and D are defined. This type of controller scheduling assumes that the matrices A, B, C, and D vary smoothly as a function of v, which is often the case in aerospace applications.

Dialog Box

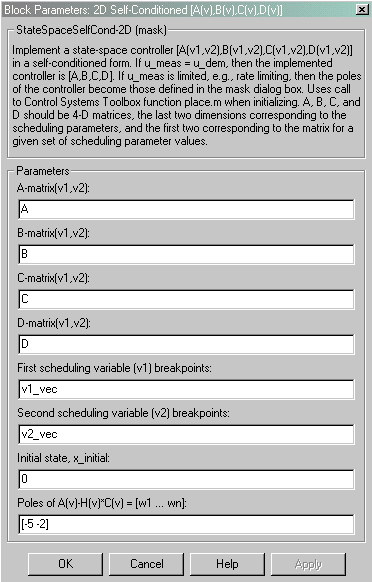
A-matrix(v1,v2): A-matrix of the state-space implementation. In the case of 2D scheduling, the A-matrix should have four dimensions, the last two corresponding to scheduling variables v1 and v2. Hence, for example, if the A-matrix corresponding to the first entry of v1 and first entry of v2 is the identity matrix, then A(:,:,1,1) = [1 0;0 1];.
B-matrix(v1,v2): B-matrix of the state-space implementation. In the case of 2D scheduling, the B-matrix should have four dimensions, the last two corresponding to scheduling variables v1 and v2. Hence, for example, if the B-matrix corresponding to the first entry of v1 and first entry of v2 is the identity matrix, then B(:,:,1,1) = [1 0;0 1];.
C-matrix(v1,v2): C-matrix of the state-space implementation. In the case of 2D scheduling, the C-matrix should have four dimensions, the last two corresponding to scheduling variables v1 and v2. Hence, for example, if the C-matrix corresponding to the first entry of v1 and first entry of v2 is the identity matrix, then C(:,:,1,1) = [1 0;0 1];.
D-matrix(v1,v2): D-matrix of the state-space implementation. In the case of 2D scheduling, the D-matrix should have four dimensions, the last two corresponding to scheduling variables v1 and v2. Hence, for example, if the D-matrix corresponding to the first entry of v1 and first entry of v2 is the identity matrix, then D(:,:,1,1) = [1 0;0 1];.
First scheduling variable (v1) breakpoints: Vector of the breakpoints for the first scheduling variable. The length of v1 should be same as the size of the third dimension of A, B, C, and D.
Second scheduling variable (v2) breakpoints: Vector of the breakpoints for the second scheduling variable. The length of v2 should be same as the size of the fourth dimension of A, B, C, and D.
Initial state, x_initial: Vector of initial states for the controller, i.e., initial values for the state vector, x. It should have length equal to the size of the first dimension of A.
Poles of A(v)-H(v)*C(v): Vector of the desired poles of A-HC. Note that the poles are assigned to the same locations for all values of the scheduling parameter, v. Hence the number of pole locations defined should be equal to the length of the first dimension of the A-matrix.

Inputs and Outputs

The first input is the measurements.

The second and third inputs are the scheduling variables ordered conforming to the dimensions of the state-space matrices.

The fourth input is the measured actuator position.

The output is the actuator demands.

Assumptions and Limitations

If the scheduling parameter inputs to the block goes out of range, then they are clipped; i.e., the state-space matrices are not interpolated out of range.

This block requires the Control Systems Toolbox.

References

The algorithm used to determine the matrix H is defined in Kautsky, Nichols, and Van Dooren, "Robust Pole Assignment in Linear State Feedback," International Journal of Control, Vol. 41, No. 5, pages 1129-1155, 1985.

2D Controller [A(v),B(v),C(v),D(v)]

2D Controller Blend

2D Observer Form [A(v),B(v),C(v),F(v),H(v)]

3D Self-Conditioned [A(v),B(v),C(v),D(v)]

2D Observer Form [A(v),B(v),C(v),F(v),H(v)] 3D Controller [A(v),B(v),C(v),D(v)]