| Aerospace Blockset |
  |
2D Observer Form [A(v),B(v),C(v),F(v),H(v)]
Implement a gain-scheduled state-space controller in an observer form depending on two scheduling parameters
Library
GNC
Description

The 2D Observer Form [A(v),B(v),C(v),F(v),H(v)] block implements a gain-scheduled state-space controller defined in the following observer form:
The main application of these blocks is to implement a controller designed using H-infinity loop-shaping, one of the design methods supported by the 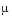 -Analysis and Synthesis Toolbox.
-Analysis and Synthesis Toolbox.
Dialog Box
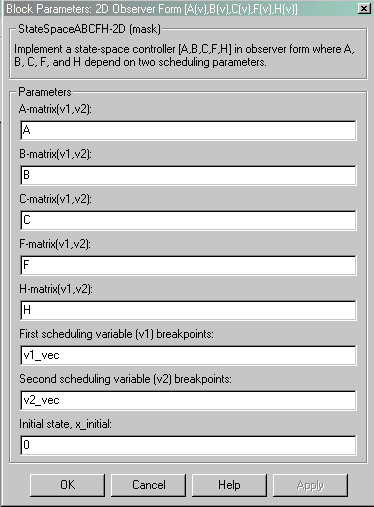
- A-matrix(v1,v2)
- A-matrix of the state-space implementation. In the case of 2D scheduling, the A-matrix should have four dimensions, the last two corresponding to scheduling variables v1 and v2. Hence, for example, if the A-matrix corresponding to the first entry of v1 and first entry of v2 is the identity matrix, then A(:,:,1,1) = [1 0;0 1];.
- B-matrix(v1,v2)
- B-matrix of the state-space implementation. In the case of 2D scheduling, the B-matrix should have four dimensions, the last two corresponding to scheduling variables v1 and v2. Hence, for example, if the B-matrix corresponding to the first entry of v1 and first entry of v2 is the identity matrix, then B(:,:,1,1) = [1 0;0 1];.
- C-matrix(v1,v2)
- C-matrix of the state-space implementation. In the case of 2D scheduling, the C-matrix should have four dimensions, the last two corresponding to scheduling variables v1 and v2. Hence, for example, if the C-matrix corresponding to the first entry of v1 and first entry of v2 is the identity matrix, then C(:,:,1,1) = [1 0;0 1];.
- F-matrix(v1,v2)
- State-feedback matrix. In the case of 2D scheduling, the F-matrix should have four dimensions, the last two corresponding to scheduling variables v1 and v2. Hence, for example, if the F-matrix corresponding to the first entry of v1 and first entry of v2 is the identity matrix, then F(:,:,1,1) = [1 0;0 1];.
- H-matrix(v1,v2)
- Observer (output injection) matrix. In the case of 2D scheduling, the H-matrix should have four dimensions, the last two corresponding to scheduling variables v1 and v2. Hence, for example, if the H-matrix corresponding to the first entry of v1 and first entry of v2 is the identity matrix, then H(:,:,1,1) = [1 0;0 1];.
- First scheduling variable (v1) breakpoints
- Vector of the breakpoints for the first scheduling variable. The length of v1 should be same as the size of the third dimension of A, B, C, F, and H.
- Second scheduling variable (v2) breakpoints
- Vector of the breakpoints for the second scheduling variable. The length of v2 should be same as the size of the fourth dimension of A, B, C, F, and H.
- Initial state, x_initial
- Vector of initial states for the controller, i.e., initial values for the state vector, x. It should have length equal to the size of the first dimension of A.
Inputs and Outputs
The first input is the set-point error.
The second and third inputs are the scheduling variables ordered conforming to the dimensions of the state-space matrices.
The fourth input is measured actuator position.
The output is the actuator demands.
Assumptions and Limitations
If the scheduling parameter inputs to the block goes out of range, then they are clipped; i.e., the state-space matrices are not interpolated out of range.
Examples
See the observer implementation within the aeroblk_HL20.mdl demo.
References
Hyde, R.A., "H-infinity Aerospace Control Design - A VSTOL Flight Application," Springer Verlag, Advances in Industrial Control Series, 1995. ISBN 3-540-19960-8. See Chapter 6.
See Also
1D Controller [A(v),B(v),C(v),D(v)]
2D Controller [A(v),B(v),C(v),D(v)]
2D Controller Blend
2D Self-Conditioned [A(v),B(v),C(v),D(v)]
3D Observer Form [A(v),B(v),C(v),F(v),H(v)]
 | 2D Controller Blend | | 2D Self-Conditioned [A(v),B(v),C(v),D(v)] |  |





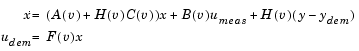
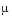 -Analysis and Synthesis Toolbox.
-Analysis and Synthesis Toolbox.
