MATLAB Function Reference

pdepe

Solve initial-boundary value problems for systems of parabolic and elliptic partial differential equations (PDEs) in one space variable and time

Syntax

• sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan)
  sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options)
  sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options,p1,p2...)
  

Arguments

m	A parameter corresponding to the symmetry of the problem. m can be slab = 0, cylindrical = 1, or spherical = 2.
pdefun	A function that defines the components of the PDE.
icfun	A function that defines the initial conditions.
bcfun	A function that defines the boundary conditions.
xmesh	A vector [x0, x1, ..., xn] specifying the points at which a numerical solution is requested for every value in tspan. The elements of xmesh must satisfy x0 < x1 < ... < xn. The length of xmesh must be >= 3.
tspan	A vector [t0, t1, ..., tf] specifying the points at which a solution is requested for every value in xmesh. The elements of tspan must satisfy t0 < t1 < ... < tf. The length of tspan must be >= 3.
options	Some options of the underlying ODE solver are available in pdepe: RelTol, AbsTol, NormControl, InitialStep, and MaxStep. In most cases, default values for these options provide satisfactory solutions. See odeset for details.
p1,p2,...	Optional parameters to be passed to pdefun, icfun, and bcfun.

Description

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan) solves initial-boundary value problems for systems of parabolic and elliptic PDEs in the one space variable 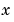and time 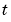. The ordinary differential equations (ODEs) resulting from discretization in space are integrated to obtain approximate solutions at times specified in tspan. The pdepe function returns values of the solution on a mesh provided in xmesh.

pdepe solves PDEs of the form:

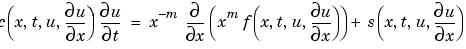
(2-1)

The PDEs hold for 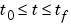and 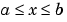. The interval 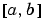must be finite. 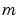can be 0, 1, or 2, corresponding to slab, cylindrical, or spherical symmetry, respectively. If 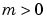, then 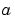must be >= 0.

In Equation 2-1, 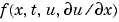is a flux term and 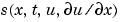is a source term. The coupling of the partial derivatives with respect to time is restricted to multiplication by a diagonal matrix 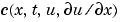. The diagonal elements of this matrix are either identically zero or positive. An element that is identically zero corresponds to an elliptic equation and otherwise to a parabolic equation. There must be at least one parabolic equation. An element of 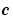that corresponds to a parabolic equation can vanish at isolated values of 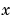if those values of 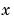are mesh points. Discontinuities in 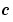and/or 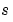due to material interfaces are permitted provided that a mesh point is placed at each interface.

For 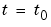and all 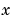, the solution components satisfy initial conditions of the form

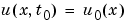
(2-2)

For all 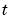and eithe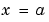r or 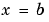, the solution components satisfy a boundary condition of the form

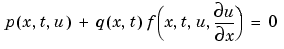
(2-3)

Elements of 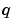are either identically zero or never zero. Note that the boundary conditions are expressed in terms of the flux 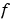rather than 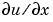. Also, of the two coefficients, only 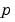can depend on .

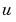In the call sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan):

• m corresponds to .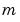
• xmesh(1) and xmesh(end) correspond to 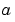and .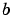
• tspan(1) and tspan(end) correspond to 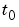and .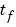
• pdefun computes the terms 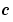, , 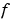and 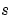(Equation 2-1). It has the form

• [c,f,s] = pdefun(x,t,u,dudx)
  

• The input arguments are scalars x and t and vectors u and dudx that approximate the solution 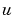and its partial derivative with respect to 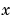, respectively. c, f, and s are column vectors. c stores the diagonal elements of the matrix 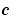(Equation 2-1).

• icfun evaluates the initial conditions. It has the form

• u = icfun(x)
  

• When called with an argument x, icfun evaluates and returns the initial values of the solution components at x in the column vector u.

• bcfun evaluates the terms 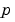and 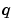of the boundary conditions (Equation 2-3). It has the form

• [pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)
  

• ul is the approximate solution at the left boundary xl = 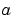and ur is the approximate solution at the right boundary xr = 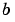. pl and ql are column vectors corresponding to 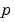and 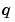evaluated at xl, similarly pr and qr correspond to xr. When 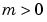and 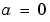, boundedness of the solution near 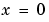requires that the flux 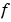vanish at 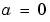. pdepe imposes this boundary condition automatically and it ignores values returned in pl and ql.

pdepe returns the solution as a multidimensional array sol. 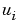 = ui = sol(:,:,i) is an approximation to the ith component of the solution vector 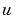. The element ui(j,k) = sol(j,k,i) approximates 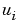at 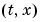 = (tspan(j),xmesh(k)).

ui = sol(j,:,i) approximates component i of the solution at time tspan(j) and mesh points xmesh(:). Use pdeval to compute the approximation and its partial derivative 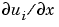at points not included in xmesh. See pdeval for details.

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options) solves as above with default integration parameters replaced by values in options, an argument created with the odeset function. Only some of the options of the underlying ODE solver are available in pdepe: RelTol, AbsTol, NormControl, InitialStep, and MaxStep. The defaults obtained by leaving off the input argument options will generally be satisfactory. See odeset for details.

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options,p1,p2...) passes the additional parameters p1, p2, ... to the functions pdefun, icfun, and bcfun. Use options = [] as a placeholder if no options are set.

Remarks

• The arrays xmesh and tspan play different roles in pdepe.

• tspan - The pdepe function performs the time integration with an ODE solver that selects both the time step and formula dynamically. The elements of tspan merely specify where you want answers and the cost depends weakly on the length of tspan.

  xmesh - Second order approximations to the solution are made on the mesh specified in xmesh. Generally, it is best to use closely spaced mesh points where the solution changes rapidly. pdepe does not select the mesh in 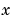automatically. You must provide an appropriate fixed mesh in xmesh. The cost depends strongly on the length of xmesh. When 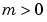, it is not necessary to use a fine mesh near 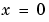to account for the coordinate singularity.

• The time integration is done with ode15s. pdepe exploits the capabilities of ode15s for solving the differential-algebraic equations that arise when Equation 2-1 contains elliptic equations, and for handling Jacobians with a specified sparsity pattern.
• After discretization, elliptic equations give rise to algebraic equations. If the elements of the initial conditions vector that correspond to elliptic equations are not "consistent" with the discretization, pdepe tries to adjust them before beginning the time integration. For this reason, the solution returned for the initial time may have a discretization error comparable to that at any other time. If the mesh is sufficiently fine, pdepe can find consistent initial conditions close to the given ones. If pdepe displays a message that it has difficulty finding consistent initial conditions, try refining the mesh.

• No adjustment is necessary for elements of the initial conditions vector that correspond to parabolic equations.

Examples

Example 1. This example illustrates the straightforward formulation, computation, and plotting of the solution of a single PDE.

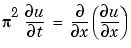
This equation holds on an interval 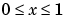for times .

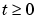The PDE satisfies the initial condition

and boundary conditions

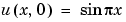
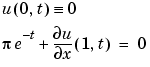
It is convenient to use subfunctions to place all the functions required by pdepe in a single M-file.

• function pdex1
  
  m = 0;
  x = linspace(0,1,20);
  t = linspace(0,2,5);
  
  sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);
  % Extract the first solution component as u.
  u = sol(:,:,1);
  
  % A surface plot is often a good way to study a solution.
  surf(x,t,u)    
  title('Numerical solution computed with 20 mesh points.')
  xlabel('Distance x')
  ylabel('Time t')
  
  % A solution profile can also be illuminating.
  figure
  plot(x,u(end,:))
  title('Solution at t = 2')
  xlabel('Distance x')
  ylabel('u(x,2)')
  % --------------------------------------------------------------
  function [c,f,s] = pdex1pde(x,t,u,DuDx)
  c = pi^2;
  f = DuDx;
  s = 0;
  % --------------------------------------------------------------
  function u0 = pdex1ic(x)
  u0 = sin(pi*x);
  % --------------------------------------------------------------
  function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)
  pl = ul;
  ql = 0;
  pr = pi * exp(-t);
  qr = 1;
  

In this example, the PDE, initial condition, and boundary conditions are coded in subfunctions pdex1pde, pdex1ic, and pdex1bc.

The surface plot shows the behavior of the solution.

The following plot shows the solution profile at the final value of t (i.e., t = 2).

Example 2. This example illustrates the solution of a system of PDEs. The problem has boundary layers at both ends of the interval. The solution changes rapidly for small .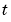

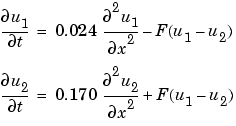
The PDEs are

where

.

This equation holds on an interval 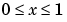for times .

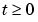The PDE satisfies the initial conditions

and boundary conditions

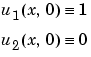
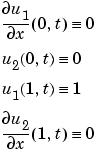
In the form expected by pdepe, the equations are

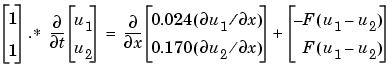
The boundary conditions on the partial derivatives of 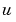have to be written in terms of the flux. In the form expected by pdepe, the left boundary condition is

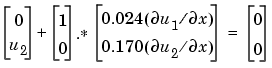
and the right boundary condition is

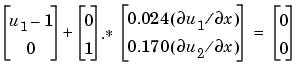
The solution changes rapidly for small 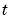. The program selects the step size in time to resolve this sharp change, but to see this behavior in the plots, the example must select the output times accordingly. There are boundary layers in the solution at both ends of [0,1], so the example places mesh points near 0 and 1 to resolve these sharp changes. Often some experimentation is needed to select a mesh that reveals the behavior of the solution.

• function pdex4
  m = 0;
  x = [0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
  t = [0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];
  
  sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
  u1 = sol(:,:,1);
  u2 = sol(:,:,2);
  
  figure
  surf(x,t,u1)
  title('u1(x,t)')
  xlabel('Distance x')
  ylabel('Time t')
  
  figure
  surf(x,t,u2)
  title('u2(x,t)')
  xlabel('Distance x')
  ylabel('Time t')
  % --------------------------------------------------------------
  function [c,f,s] = pdex4pde(x,t,u,DuDx)
  c = [1; 1];                                  
  f = [0.024; 0.17] .* DuDx;                   
  y = u(1) - u(2);
  F = exp(5.73*y)-exp(-11.47*y);
  s = [-F; F];                                                          
  % --------------------------------------------------------------
  function u0 = pdex4ic(x);
  u0 = [1; 0];                                 
  % --------------------------------------------------------------
  function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
  pl = [0; ul(2)];                               
  ql = [1; 0];                                  
  pr = [ur(1)-1; 0];                            
  qr = [0; 1];                                  
  

In this example, the PDEs, intial conditions, and boundary conditions are coded in subfunctions pdex4pde, pdex4ic, and pdex4bc.

The surface plots show the behavior of the solution components.

See Also

function_handle, pdeval, ode15s, odeset, odeget

References

[1]  Skeel, R. D. and M. Berzins, "A Method for the Spatial Discretization of Parabolic Equations in One Space Variable," SIAM Journal on Scientific and Statistical Computing, Vol. 11, 1990, pp.1-32.

pcolor

pdeval