Signal Processing Toolbox

統計的信号処理

相関と共分散

Signal Processing Toolboxは、ランダム信号の重要な機能を推定するためのツールを用意しています。特に、相関列と共分散列を推定するツール、および、離散信号のスペクトル密度関数を推定するツールを用意しています。本章では、相関関数と共分散関数について説明し、パワースペクトルを推定するための数学的に関連する関数について検討します。

関数xcorr、および、xcovは、ランダムプロセスの相互相関列と相互共分散列を推定します。これらは、また、特殊な場合として、自己相関、自己共分散を扱うこともできます。

真の相互相関列は、つぎのように定義される統計的な量です。

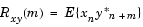
ここで、x_nとy_nは、定常のランダムプロセスであり、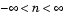です。また、E{·}は期待値演算子です。相互共分散列は平均を除去したものの相互相関列であり、つぎのように定義されます。

あるいは、相互相関で表すと、つぎのようになります。

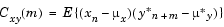
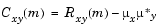
実際には、無限長のランダムプロセスから有限部分しか利用することができないため、これらの列を推定することになります。x_nおよび y_nのNサンプルに基づいた一般的な推定は、確定的な相互相関列になります（時間不確定関数とも呼ばれます）。

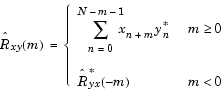
ここで、x_nおよびy_nには0からN-1までのインデックス、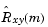には、-(N-1)からN-1までのインデックスが付いているものと仮定します。関数xcorrは、長さNのベクトル xおよび yに格納された入力x_nおよびy_nが与えられると、効果的なFFTベースのアルゴリズムを使って、この和を評価します。この操作は、2つの列の1つを時間的に逆にしたコンボリューションと等しくなります。

たとえば、

x = [1 1 1 1 1]';
y = x;
xyc = xcorr(x,y)
xyc =
    1.0000
    2.0000
    3.0000
    4.0000
    5.0000
    4.0000
    3.0000
    2.0000
    1.0000

得られた列は、入力列の長さの2倍から1を引いたものになることに注目してください。従って、N番目の要素は遅れ0での相関となります。また、2つの矩形パルスのコンボリューションを行うと、三角パルスが出力されることに注目してください。

関数xcovは、自己共分散列、および、相互共分散列を推定します。この関数は、xcorrと同じオプションをもち、同じ和を計算しますが、まずxとyの平均を最初に取り除き、それに対して計算しています。

参考文献

バイアスと正規化