Signal Processing Toolbox

スペクトル解析

スペクトル推定 の目的は、有限長のデータをベースに、信号内に含まれているエネルギーの分布(周波数上)を記述することです。パワースペクトルの推定は、広い帯域に分布する雑音の中に含まれている信号の検出を含む、種々のアプリケーションで有効です。

定常ランダムプロセス x_n の パワースペクトル は、離散時間フーリエ変換による相関列と数学的に関連しています。正規化された周波数を使って、つぎのように表わせます。

これは、物理的な周波数 f の関数(たとえば、ヘルツ単位)と、 = 2f/f_s の関係を使って、関連付けられます。ここで、f_s は、サンプリング周期です。

相関列は、逆離散フーリエ変換を使って、パワースペクトルから引き出すことができます。

データ列 x_n のナイキスト区間までの平均パワーは、つぎのように表わせます。

上の表現で使われる量

は、定常ランダム信号 x_n の パワースペクトル密度(PSD) として定義されます。

特定の周波数帯域 [₁, ₂], に渡る信号の平均パワーは、その区間の PSD の積分より求められます。

P_xx() は、無限小 周波数帯域での信号のパワー部分を表現します。これが、パワースペクトル 密度 と言われる理由です。

PSD の単位は、単位周波数に対するパワー(すなわち、ワット)です。P_xx() の場合、これは、watts/rad/sample、または、単に、watts/rad です。P_xx(f) の場合、単位は、watts/hertz です。周波数に関する PSD の積分は、平均パワー に対して、期待されるように、watts の単位で表わせます。

実信号に対して、PSD は、DC を中心に対称です。そのために、0 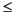< に対して、P_xx() のみで、PSD の特徴を十分に表わすことができます。しかし、ナイキストまでの区間に関する平均パワーを得るためには、 片側 PSD の考えを導入する必要があります。

片側 PSD は、つぎの表現を使って表わせます。

周波数帯域 [₁, ₂], での信号の平均パワーは、つぎのように片側 PSD を使って、計算できます。

マルチチャンネル

スペクトル推定法の概要