Signal Processing Toolbox

MUSIC法および固有ベクトル解析法

関数pmusicは、つぎの2つの関連するスペクトル解析法を提供します。

• Schmidtによって開発された多重信号分類法(MUSIC)
• Johnsonによって開発された固有ベクトル(EV)法

これらの方法の概要については、Marple [2] (pgs.373-378)を参照してください。

これらの方法はいずれも、自己相関行列の固有解析に基づく周波数推定手法です。このタイプのスペクトル解析では、情報を相関行列かまたはデータ行列に類別し、さらに信号部分空間かまたは雑音部分空間に分類します。

固有解析の概要

複数の複素正弦波と白色雑音からなるデータを考えます。このシステムの自己相関行列Rは、つぎのように信号の自己相関行列(S)と雑音の自己相関行列(W)の和として記述することができます。

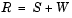
信号の自己相関行列の固有ベクトルと信号および雑音の部分空間の固有ベクトルとの間には、密接な関係があります。Sの固有ベクトルvは、信号ベクトルと同じ信号部分空間を形成します。システムがM個の複素正弦波を含み、自己相関行列の次数がpの場合、固有ベクトルv_M+1からv_p+1は、自己相関行列の雑音部分空間を形成します。

この周波数推定を行なうため、固有解析法は、信号部分空間と雑音部分空間で、あるベクトル関数を計算します。MISIC法とEV法共に、入力信号の中で、それが保有する正弦波の周波数の1つで、その関数が理論的に無限大になるように設定しています。ディジタル技術を使って、得られる推定値は問題となる周波数のところで鋭いピークを示しますが、これは、ベクトル内には無限大になるものが存在していないことを示すものです。

MUSIC推定は、つぎの公式により得られます。

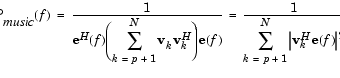
ここで、Nは固有ベクトルの大きさ、e(f)は複素正弦波ベクトルです。

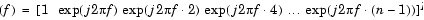
vは、入力信号の相関行列の固有ベクトルを表します。すなわち、 v_k は、k番目の固有ベクトルで、Hは共役転置演算子です。総和の計算で使われている固有ベクトルは、最小の固有値に対応し、雑音部分空間を形成します(pは、信号部分空間の大きさです)。

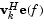　は、フーリエ変換(ベクトルe(f)は複素指数)と等しくなります。この形式は、各v_kについてFFTを計算して、ゲインの2乗を加算することができるため、数値計算に有効です。

EV法では、つぎのように相関行列の固有値を使って、和に重みを付けます。

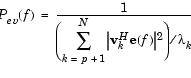
このツールボックスの関数pmusicは、信号の場合には関数svd(特異値分解)を、相関行列の解析には関数eigを使い、固有ベクトルを信号部分空間と雑音部分空間に割り当てます。svdを使用する場合は、pmusicが明示的に相関行列を計算することは全くなく、特異値が固有値となります。

部分空間閾値の制御

ユーザが信号および雑音の部分空間へ固有ベクトルを割り当てるための基準は、関数pmusicでは、閾値引数threshを使います。threshは、2要素のベクトルで、最初の要素は信号部分空間を形成する固有ベクトル数、2番目の要素は閾値に関するものです。

• thresh(2) 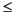1の場合、 thresh(1)は信号部分空間を形成する固有ベクトル数を設定します。この場合、thresh(1)の値は、範囲[0, N)内になければなりません。ここで、 Nはつぎのいずれかです。
• xRがデータ行列の場合は、xRの列数
• xRが相関行列の場合は、行列の大きさ
• xRが信号ベクトルの場合は、ウィンドウ長
• thresh(1)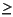N で、かつ、 thresh(2)の場合、thresh(2)は信号部分空間と雑音部分空間との間の固有値を分ける絶対閾値を設定する1以上の値となります。すなわち、与えられた 固有値が積thresh(2)min{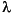_k}以下ならば、その固有ベクトルは雑音部分空間に割り当てられます。
• thresh(1)<Nかつthresh(2)が1に等しいか、または、大きい場合、 thresh(1)は、やはり信号部分空間内の 固有ベクトル数の最大数を設定します。ただし、thresh(2)で設定された閾値に関する値は、雑音部分空間に固有ベクトルを割り当てることもできます。
• thresh(1)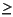N かつ thresh(2)1に等しいかまたは小さい場合、雑音を表す固有ベクトルはありません。これは、意味のない場合で、pmusicはエラーを出力します。

引数threshの使用法の詳細については、第6章のpmusicのリファレンスを参照してください。

共分散法と修正共分散法

参考文献