Signal Processing Toolbox

周波数領域ベースのモデリング

関数invfreqsおよび関数invfreqzは、freqsおよびfreqzの逆演算を実行する関数、すなわち、与えられた複素周波数応答に一致するように設定した設定次数のアナログまたはディジタル伝達関数を求めます。つぎの例題では、invfreqzを示していますが、この考察はinvfreqsにも適用されます。

[b,a] = butter(4,.4)    % Butterworthローパスフィルタの設計
b =
    0.0466    0.1863    0.2795    0.1863    0.0466
a =
    1.0000   -0.7821    0.6800   -0.1827    0.0301
[h,w] = freqz(b,a,64);         % 周波数応答の計算
[bb,aa] = invfreqz(h,w,4,4)    % モデル: nb = 4、na = 4
bb =
    0.0466    0.1863    0.2795    0.1863    0.0466
aa =
    1.0000   -0.7821    0.6800   -0.1827    0.0301

周波数ベクトルw はラジアン/秒単位ですが、この周波数は、等間隔である必要はありません。invfreqzは、この周波数データを適合する任意の次数のフィルタを求めます。3次のフィルタの場合には、つぎのようになります。

[bb,aa] = invfreqz(h,w,3,3)   % 3次のIIRフィルタを求める
bb =
    0.0464    0.1785    0.2446    0.1276
aa =
    1.0000   -0.9502    0.7382   -0.2006

invfreqzとinvfreqsは、共に実数係数のフィルタを設計します。正の周波数fのデータ点に対して、これらの関数は周波数応答をfと-fの両方で適合させます。

デフォルトでは、invfreqzは誤差方程式法を用いて、データから最良のモデルを同定します。これは、次式

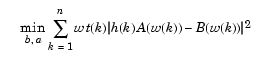
で連立1次方程式を作成し、MATLABの\演算子で解くことにより、bとaを求めるものです。ここで、A(w(k)) およびB(w(k)) は、それぞれ周波数w(k)での多項式aおよびbのフーリエ変換であり、nは周波数点数(hおよびwの長さ)です。wt(k) により、周波数点間での誤差に対して重みを付けることができます。ステートメント

invfreqz(h,w,nb,na,wt)

は、重みベクトルを含んでいます。このモードでは、invfreqzから得られるフィルタが安定であるという保証はありません。

invfreqzは、実際の周波数応答点と希望の応答との間の2乗誤差に重みを付けたものの和を最小にする直接的な問題を解く優れた("出力誤差")アルゴリズムを使っています。

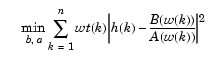
このアルゴリズムを使用するには、つぎのように重みベクトルパラメータの後に反復回数を入力引数として設定します。

wt = ones(size(w));    % 重み1つのベクトルの作成
[bbb,aaa] = invfreqz(h,w,3,3,wt,30)  % 30回の反復
bbb =
    0.0464    0.1829    0.2572    0.1549
aaa =
    1.0000   -0.8664    0.6630   -0.1614

得られるフィルタは常に安定しています。

[H1,w] = freqz(b,a);
[H2] = freqz(bb,aa);
[H3] = freqz(bbb,aaa);
s.plot = 'mag';
s.xunits = 'rad/sample';
s.yunits = 'linear';
freqzplot([H1 H2 H3],w);
legend('Original','First Estimate','Second Estimate',3);
grid on

数値的な適合の優位性を検証するには、つぎのようにします。

sum(abs(h-freqz(bb,aa,w)).^2)   % アルゴリズム1、全誤差
ans =
    0.0200
sum(abs(h-freqz(bbb,aaa,w)).^2) % アルゴリズム2、全誤差
ans =
    0.0096

時間領域ベースのモデリング

リサンプリング